Log link in Poisson ash
Table of Contents
Introduction
We previously found several instances of genes which clearly exhibit unimodal expression variation (by inspection), but significantly depart from the estimated unimodal distribution
\begin{align*} x_i \mid s_i, \lambda_i &\sim \operatorname{Poisson}(s_i \lambda_i)\\ \lambda_i &\sim g(\cdot) = \sum_{k=1}^K w_k \operatorname{Uniform}(\lambda_0, a_k) \end{align*}where \(\lambda_0\) is the mode and we abuse notation to allow endpoints \(a_k < \lambda_0\). One feature which appears to be common to these examples is estimating the density near zero wrong, such that the smallest randomized quantiles deviate from uniform.
Here, we investigate problems in fitting a unimodal assumption under the log link
\begin{align*} x_i \mid s_i, \lambda_i &\sim \operatorname{Poisson}(s_i \lambda_i)\\ \theta_i = \ln \lambda_i &\sim g(\cdot) = \sum_{k=1}^K w_k \operatorname{Uniform}(\theta_0, a_k) \end{align*}Setup
import numpy as np import pandas as pd import rpy2.robjects import rpy2.robjects.pandas2ri import scipy.integrate as si import scipy.special as sp import scipy.stats as st rpy2.robjects.pandas2ri.activate()
%matplotlib inline %config InlineBackend.figure_formats = set(['retina'])
import matplotlib.pyplot as plt plt.rcParams['figure.facecolor'] = 'w' plt.rcParams['font.family'] = 'Nimbus Sans'
Derivations
Under the log link, we have
\begin{align*} x_i \mid s_i, \lambda_i &\sim \operatorname{Poisson}(s_i \lambda_i)\\ \theta_i = \ln \lambda_i &\sim \operatorname{Uniform}(a, b) \end{align*}and
\begin{align*} \Pr(x_i = x) &= \frac{1}{b - a} \int_a^b \operatorname{Poisson}(x; \exp(\ln s_i + \theta_i))\,d\theta_i\\ &= \frac{1}{b - a} \int_a^b \frac{(s_i)^x}{\Gamma(x + 1)} \exp(\theta_i)^{x}\exp(-s_i \exp(\theta_i))\,d\theta_i\\ &= \frac{1}{x (b - a)} \int_{\exp(a)}^{\exp(b)} \frac{(s_i)^x}{\Gamma(x)} \lambda_i^{x - 1}\exp(-s_i \lambda_i)\,d\lambda_i\\ &= \frac{1}{x (b - a)} \left( F_\Gamma(\exp(b); x, s_i) - F_\Gamma(\exp(a); x, s_i) \right)\\ \Pr(x_i \leq x) &= \sum_{k=0}^{x} \frac{1}{k (b - a)} \left( F_\Gamma(\exp(b); k, s_i) - F_\Gamma(\exp(a); k, s_i) \right) \end{align*}where \(F_\Gamma(\cdot; \alpha, \beta)\) denotes the CDF of the Gamma distribution with shape \(\alpha\) and rate \(\beta\). This derivation breaks down for \(\Pr(x_i = 0)\), because the Gamma distribution is not defined for \(\alpha = 0\), and because there is a factor of \(1 / x_i\). Instead,
\begin{align*} \Pr(x_i = 0) &= \frac{1}{b - a} \int_{\exp(a)}^{\exp(b)} \frac{\exp(-s_i \lambda_i)}{\lambda_i}\,d\lambda_i\\ &= \frac{1}{b - a} \int_{-s_i \exp(a)}^{-s_i \exp(b)} \frac{\exp(t)}{t}\,dt\\ &= \frac{\operatorname{Ei}(-s_i \exp(b)) - \operatorname{Ei}(-s_i \exp(a))}{b - a} \end{align*}where \(\operatorname{Ei}\) is the exponential integral.
Compare the estimate of \(\ln \Pr(x_i = 0 \mid x_i+)\) using numerical integration, the special case analytic formula involving \(\operatorname{Ei}\), and introducing a pseudocount into the formula involving \(F_\Gamma\).
# Typical values s = np.logspace(0, 6, 20) a = np.log(2e-3) b = np.log(3e-3) # Numerical integration px_0 = np.array([si.quad(lambda x: st.poisson(mu=s_j * np.exp(x)).pmf(0), a, b)[0] / (b - a) for s_j in s]) # Analytic px_1 = (sp.expi(-s * np.exp(b)) - sp.expi(-s * np.exp(a))) / (b - a) # Follow ashr eps = 1e-5 F = st.gamma(a=eps, scale=1 / s).cdf px_2 = (F(np.exp(b)) - F(np.exp(a))) / (eps * (b - a)) np.log(pd.DataFrame({'quad': px_0, 'Ei': px_1, 'F_gamma': px_2}, index=s))
quad Ei F_gamma 1.000000 -0.002466 -0.002466 -0.002521 2.069138 -0.005103 -0.005103 -0.005150 4.281332 -0.010558 -0.010558 -0.010598 8.858668 -0.021845 -0.021845 -0.021877 18.329807 -0.045193 -0.045193 -0.045218 37.926902 -0.093480 -0.093480 -0.093498 78.475997 -0.193290 -0.193290 -0.193301 162.377674 -0.399380 -0.399380 -0.399383 335.981829 -0.823968 -0.823968 -0.823964 695.192796 -1.694739 -1.694739 -1.694728 1438.449888 -3.464673 -3.464673 -3.464655 2976.351442 -7.008214 -7.008214 -7.008189 6158.482111 -13.999734 -13.999734 -13.999714 12742.749857 -27.858046 -27.858046 -inf 26366.508987 -55.813991 -55.813991 -inf 54555.947812 -112.910591 -112.910591 -inf 112883.789168 -230.288764 -230.288764 -inf 233572.146909 -472.390342 -472.390345 -inf 483293.023857 -inf -inf -inf 1000000.000000 -inf -inf -inf
Matthew Stephens provided an alternative derivation:
\begin{align*} \Pr(x_i = x) &= \frac{1}{b - a} \int_a^b \operatorname{Poisson}(x; \exp(\ln s_i + \theta_i))\,d\theta_i\\ &= \frac{1}{b - a} \int_{\exp(a)}^{\exp(b)} \frac{s_i^x}{\Gamma(x + 1)} \lambda_i^{x - 1}\exp(-s_i \lambda_i)\,d\lambda_i\\ &= \frac{1}{\Gamma(x + 1) (b - a)} \int_{s_i \exp(a)}^{s_i \exp(b)} u^{x-1} \exp(-u)\,du\\ &= \frac{1}{\Gamma(x + 1) (b - a)} \left( \Gamma(x, s_i \exp(a)) - \Gamma(x, s_i \exp(b)) \right) \end{align*}where \(\Gamma(\cdot, \cdot)\) is the upper incomplete Gamma function. The resulting expression is defined for all \(x \geq 0\).
Results
Simulated data
Simulate some near-NB ZINB data.
dat <- readRDS("/scratch/midway2/aksarkar/modes/test-data/pois-mode-est.Rds") with(dat, summary(MASS::glm.nb(x ~ offset(log(s))))$twologlik / 2)
-2008.50373054974
Fit ash_pois using identity link.
fit0 <- ashr::ash_pois(dat$x, dat$s, link="identity", mixcompdist="halfuniform") fit0$loglik
-2008.27125771255
Implement
autoselect.mixsd for log link.
Fit ash_pois using log link. (The problem turned out to be
mode
estimation limits.)
fit1 <- ashr::ash_pois(dat$x, dat$s, link="log", mixcompdist="halfuniform") fit1$loglik
-2008.26590367036
Real data
Load a real data example which is clearly unimodal, but departs from the fitted distribution.
dat <- readRDS("/scratch/midway2/aksarkar/modes/test-data/b-cell-data.Rds") query <- dat[dat["gene"] == "ENSG00000019582",]
data = pd.DataFrame(rpy2.robjects.r['readRDS']("/scratch/midway2/aksarkar/modes/test-data/b-cell-data.Rds")) query = data[data["gene"] == "ENSG00000019582"]
Plot the empirical distribution of molecule counts.
plt.clf() plt.gcf().set_size_inches(3, 3) plt.hist(query['count'], bins=np.arange(query['count'].max() + 1), color='k') plt.xlabel('Number of molecules') plt.ylabel('Number of cells') plt.tight_layout()
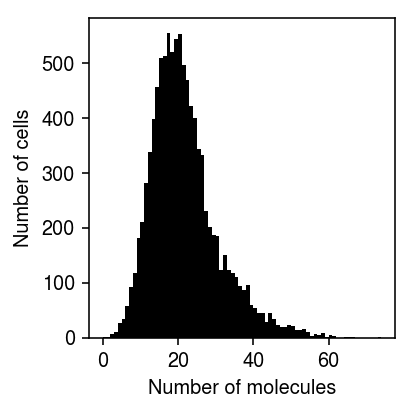
Plot the distribution of MLEs \(x_i / s_i\).
plt.clf() plt.gcf().set_size_inches(3, 3) plt.hist(query['count'] / query['size'], bins=100, color='k') plt.xlabel('$\hat\lambda_i$') plt.ylabel('Number of cells') plt.tight_layout()
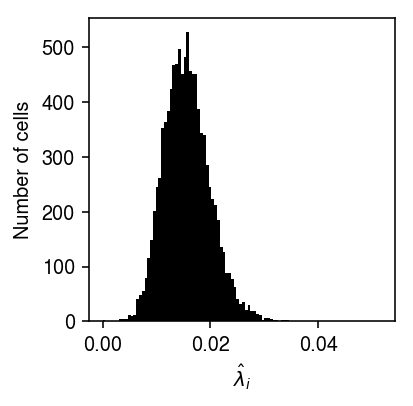
As a baseline, fit a Gamma assumption.
with(query, summary(MASS::glm.nb(count ~ offset(log(size))))$twologlik / 2)
-31414.5999341206
Fit a unimodal assumption under the identity link.
fit0 <- ashr::ash_pois(query$count, query$size, link="identity", mixcompdist="halfuniform") fit0$loglik
-31395.0538031464
Report the diagnostic test statistic and p-value.
zgrep -wm1 ENSG00000019582 /project2/mstephens/aksarkar/projects/singlecell-modes/data/gof/b_cells-unimodal.txt.gz
Fit a unimodal assumption under the log link.
fit1 <- ashr::ash_pois(query$count, query$size, link="log", mixcompdist="halfuniform") fit1$loglik
-31394.8462180293
Make sure the marginal PMF is sensible. (This was not implemented correctly before.)
any(fit1$fitted_g$pi %*% ashr:::comp_dens_conv(fit1$fitted_g, fit1$data) > 1)
FALSE
any(ashr:::comp_dens_conv(fit1$fitted_g, fit1$data) > 1)
FALSE
Implement the diagnostic for the log link.
fx = fit1$fitted_g$pi %*% ashr:::comp_dens_conv(fit1$fitted_g, fit1$data) N = nrow(query) K = length(fit1$fitted_g$a) ## Important: this is F_j(x_{ij} - 1), needed for randomized quantiles Fx_1 = matrix(rep(0, N * K), N, K) for (i in 1:N) { for (k in 1:K) { if (fit1$fitted_g$pi[k] < 1e-8) { next } else if (query$count[i] == 0) { Fx_1[i, k] = 0 } else if (fit1$fitted_g$a[k] == fit1$fitted_g$b[k]) { Fx_1[i, k] = ppois(query$count[i] - 1, lambda=query$size[i] * exp(fit1$fitted_g$a[k])) } else { ak = min(fit1$fitted_g$a[k], fit1$fitted_g$b[k]) bk = max(fit1$fitted_g$a[k], fit1$fitted_g$b[k]) grid = seq(0, query$count[i] - 1) Fx_1[i, k] = sum((expint::gammainc(grid, query$size[i] * exp(ak)) - expint::gammainc(grid, query$size[i] * exp(bk))) / (gamma(grid + 1) * (bk - ak))) } } }
rpp = drop(Fx_1 %*% fit1$fitted_g$pi) + runif(n=N) * fx
ks.test(rpp, punif)$p.value
0.00683832270839435