Deconvolution of near-Poisson data
Table of Contents
Introduction
Deconvolution of Poisson data assuming a point mass is trivial:
\begin{align*} x_i &\sim \operatorname{Poisson}(s_i \lambda_i)\\ \lambda_i &\sim \delta_\mu(\cdot)\\ \hat\mu &= \frac{\sum_i x_i}{\sum_i s_i} \end{align*}More general approaches should all be able to fit this case. Here, we investigate cases where they fail.
Setup
import numpy as np import pandas as pd import scipy.special as sp import scipy.stats as st import scmodes import scqtl.simple import rpy2.robjects.packages import rpy2.robjects.pandas2ri rpy2.robjects.pandas2ri.activate() ashr = rpy2.robjects.packages.importr('ashr') descend = rpy2.robjects.packages.importr('descend')
%matplotlib inline %config InlineBackend.figure_formats = set(['retina'])
import matplotlib.pyplot as plt plt.rcParams['figure.facecolor'] = 'w' plt.rcParams['font.family'] = 'Nimbus Sans'
Results
Extract the examples.
Read the results of benchmarking deconvolution methods on homogeneous tissues.
benchmark = {} for data in ('cytotoxic_t', 'b_cells', 'ipsc'): benchmark[data] = ( pd.read_csv(f'/project2/mstephens/aksarkar/projects/singlecell-modes/data/deconv-generalization/{data}-gpu.txt.gz', index_col=0, sep='\t') .merge(pd.read_csv(f'/project2/mstephens/aksarkar/projects/singlecell-modes/data/deconv-generalization/{data}-unimodal.txt.gz', index_col=0, sep='\t'), left_index=True, right_index=True) .merge(pd.read_csv(f'/project2/mstephens/aksarkar/projects/singlecell-modes/data/deconv-generalization/{data}-zief.txt.gz', index_col=0, sep='\t'), left_index=True, right_index=True) .merge(pd.read_csv(f'/project2/mstephens/aksarkar/projects/singlecell-modes/data/deconv-generalization/{data}-npmle.txt.gz', index_col=0, sep='\t'), left_index=True, right_index=True))
Extract the genes for which ZIEF does best.
query = benchmark['b_cells'][benchmark['b_cells']['zief'] > benchmark['b_cells']['gamma']].index
Read the count matrix.
b_cells = scmodes.dataset.read_10x('/project2/mstephens/aksarkar/projects/singlecell-ideas/data/10xgenomics/b_cells/filtered_matrices_mex/hg19/', return_df=True) s = b_cells.sum(axis=1)
Read the gene metadata.
gene_info = pd.read_csv('/project2/mstephens/aksarkar/projects/singlecell-qtl/data/scqtl-genes.txt.gz', sep='\t', index_col=0)
Deconvolve specific examples
Fit various deconvolutions.
x = b_cells.loc[:,query[0]] lam = x / s K = 100 grid = np.linspace(0, lam.max(), K + 1)
gamma_res = scqtl.simple.fit_nb(x, s) zig_res = scqtl.simple.fit_zinb(x, s) unimodal_res = ashr.ash_workhorse( pd.Series(np.zeros(x.shape)), 1, outputlevel=pd.Series(['fitted_g', 'loglik']), lik=ashr.lik_pois(y=x, scale=s, link='identity'), mixsd=pd.Series(np.geomspace(lam.min() + 1e-8, lam.max(), 25)), mode=pd.Series([lam.min(), lam.max()])) zief_res = descend.deconvSingle(x, scaling_consts=s, verbose=False) npmle_res = ashr.ash_workhorse( pd.Series(np.zeros(x.shape)), 1, outputlevel=pd.Series(['fitted_g', 'loglik']), lik=ashr.lik_pois(y=x, scale=s, link='identity'), g=ashr.unimix(pd.Series(np.ones(K) / K), pd.Series(grid[:-1]), pd.Series(grid[1:])))
Discretize the CDFs.
grid = np.linspace(lam.min(), 1e-3, 1000) gamma_cdf = st.gamma(a=gamma_res[1], scale=gamma_res[0] / gamma_res[1]).cdf(grid) zig_cdf = gamma_cdf * sp.expit(-zig_res[2]) + sp.expit(zig_res[2]) unimodal_cdf = ashr.cdf_ash(unimodal_res, grid) zief_g = np.array(zief_res.slots['distribution'])[:,:2] zief_cdf = np.array([zief_g[:,0], np.cumsum(zief_g[:,1])]) npmle_cdf = ashr.cdf_ash(npmle_res, grid)
plt.clf() fig, ax = plt.subplots(2, 1) fig.set_size_inches(6, 4) ax[0].hist(x, bins=np.arange(x.max() + 1), color='k') ax[0].set_xlabel('Num mols') ax[0].set_ylabel('Num cells') cm = plt.get_cmap('Dark2').colors ax[1].set_xlim(0, 1e-3) ax[1].plot(grid, gamma_cdf, color=cm[0], lw=1, label='Gamma') ax[1].plot(grid, zig_cdf, color=cm[1], lw=1, label='ZIG') ax[1].plot(np.array(unimodal_cdf.rx2('x')), np.array(unimodal_cdf.rx2('y')).ravel(), c=cm[2], lw=1, label='Unimodal') ax[1].plot(zief_cdf[0], zief_cdf[1], c=cm[3], lw=1, label='ZIEF') ax[1].plot(np.array(npmle_cdf.rx2('x')), np.array(npmle_cdf.rx2('y')).ravel(), c=cm[4], lw=1, label='NPMLE') ax[1].set_xlabel('Latent gene expression') ax[1].set_ylabel('CDF') ax[1].legend(frameon=False) fig.tight_layout()
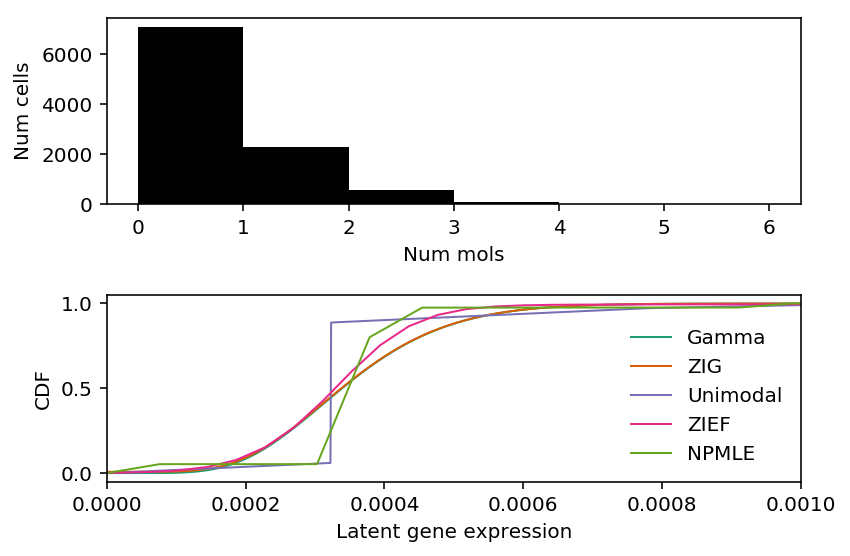
Zoom in around 0.
plt.clf() plt.gcf().set_size_inches(3, 3) cm = plt.get_cmap('Dark2').colors plt.xlim(0, 1e-4) plt.ylim(0, .1) plt.xticks([0, 5e-5, 1e-4]) plt.plot(grid, gamma_cdf, color=cm[0], lw=1, label='Gamma') plt.plot(grid, zig_cdf, color=cm[1], lw=1, label='ZIG') plt.plot(np.array(unimodal_cdf.rx2('x')), np.array(unimodal_cdf.rx2('y')).ravel(), c=cm[2], lw=1, label='Unimodal') plt.plot(zief_cdf[0], zief_cdf[1], c=cm[3], lw=1, label='ZIEF') plt.plot(np.array(npmle_cdf.rx2('x')), np.array(npmle_cdf.rx2('y')).ravel(), c=cm[4], lw=1, label='NPMLE') plt.xlabel('Latent gene expression') plt.ylabel('CDF') plt.legend(frameon=False) plt.tight_layout()
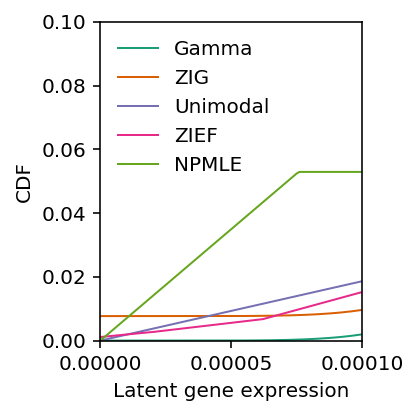
Report the training log likelihoods.
point_llik = st.poisson(mu=x.sum() / s.sum()).logpmf(x) gamma_llik = st.nbinom(n=gamma_res[1], p=1 / (1 + s * gamma_res[0] / gamma_res[1])).logpmf(x) zig_llik = np.where(x < 1, -np.log1p(np.exp(-zig_res[2])) + np.log1p(np.exp(gamma_llik - zig_res[2])), -np.log1p(np.exp(zig_res[2])) + gamma_llik) unimodal_llik = np.array(unimodal_res.rx2('loglik')) zief_llik = np.where(x < 1, np.log(st.poisson(mu=s.values.reshape(-1, 1) * zief_g[:,0]).pmf(x.values.reshape(-1, 1)).dot(zief_g[:,1])), np.log(st.poisson(mu=s.values.reshape(-1, 1) * zief_g[1:,0]).pmf(x.values.reshape(-1, 1)).dot(zief_g[1:,1]))) npmle_llik = np.array(npmle_res.rx2('loglik')) pd.Series({'Point': point_llik.sum(), 'Gamma': gamma_llik.sum(), 'ZIG': zig_llik.sum(), 'Unimodal': unimodal_llik.sum(), 'ZIEF': zief_llik.sum(), 'NPMLE': npmle_llik.sum()})
Point -31653.253236 Gamma -7702.696681 ZIG -7702.818529 Unimodal -7702.849389 ZIEF -7702.299609 NPMLE -7701.940404 dtype: float64
The reason ZIEF appeared anomalous in our benchmark was that our implementation of the validation set log likelihood, marginalizing over the estimated latent distribution \(\hat{g}\), was incorrect.
Poisson ash
Draw some near-Poisson data.
data, _ = scqtl.simulation.simulate(num_samples=1000, logodds=-5, seed=2) x = pd.Series(data[:,0]) s = pd.Series(data[:,1]) lam = x / s
Write out the data.
rpy2.robjects.r['saveRDS'](pd.DataFrame({'x': x, 's': s}), 'pois-mode-est.Rds')
rpy2.rinterface.NULL
Fit Poisson convolved with point mass.
fit0 = scqtl.simple.fit_pois(x, s)
Fit ZINB.
fit1 = scqtl.simple.fit_zinb(x, s)
Fit Poisson ash.
fit2 = ashr.ash_workhorse( # these are ignored by ash pd.Series(np.zeros(x.shape)), 1, outputlevel=pd.Series(['loglik', 'fitted_g']), lik=ashr.lik_pois(y=x, scale=s, link='identity'), mixcompdist='halfuniform', mixsd=pd.Series(np.geomspace(lam.min() + 1e-8, lam.max(), 25)))
Report the log likelihood.
pd.Series({'pointmass': fit0[-1],
'zig': fit1[-1],
'unimodal': np.array(fit2.rx2('loglik'))[0]})
pointmass -2008.663140 zig -2008.407921 unimodal -2077.552567 dtype: float64
Plot the data and estimated \(\hat{g}\). Also plot the estimated mode.
cm = plt.get_cmap('Dark2') plt.clf() fig, ax = plt.subplots(2, 1) fig.set_size_inches(5, 4) ax[0].hist(x.values, bins=np.arange(x.max() + 1), color='0.5') ax[0].set_xlim(0, x.max()) ax[0].set_xlabel('Number of molecules') ax[0].set_ylabel('Number of cells') ax[1].axvline(x=fit0[0], c=cm(0), lw=1, ls='--', label='Point mass') ax[1].plot(grid, zinb_cdf, lw=1, c=cm(1), label='ZIG') ax[1].axvline(x=fit1[0], c=cm(1), ls=':', lw=1) ax[1].plot(grid, Fx, lw=1, c=cm(2), label='Unimodal') ax[1].axvline(x=np.array(fit2.rx2('fitted_g').rx2('a'))[0], c=cm(1), ls=':', lw=1) ax[1].legend(frameon=False) ax[1].set_xlabel('Latent gene expression') ax[1].set_ylabel('CDF') fig.tight_layout()
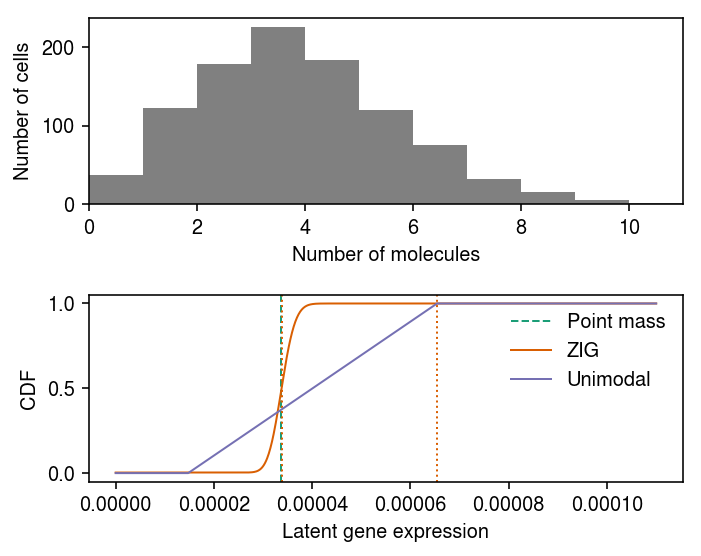
Examine mode estimation.
mode = ashr.ash_estmode( betahat=pd.Series(np.zeros(x.shape)), sebetahat=1, modemin=lam.min(), modemax=lam.max(), lik=ashr.lik_pois(y=x, scale=s, link='identity'), mixcompdist='halfuniform', mixsd=pd.Series(np.geomspace(lam.min() + 1e-8, lam.max(), 25))) mode = np.array(mode)[0] fit3 = ashr.ash_workhorse( # these are ignored by ash pd.Series(np.zeros(x.shape)), 1, outputlevel=pd.Series(['loglik', 'fitted_g']), lik=ashr.lik_pois(y=x, scale=s, link='identity'), mixcompdist='halfuniform', mixsd=pd.Series(np.geomspace(lam.min() + 1e-8, lam.max(), 25)), mode=mode)
Evaluate the ash log likelihood on a grid of modes, over the space that
ash.estmode optimizes over.
grid = np.linspace(lam.min(), lam.max(), 1000)[1:]
llik = [] for l in grid: fit = ashr.ash_workhorse( # these are ignored by ash pd.Series(np.zeros(x.shape)), 1, outputlevel=pd.Series(['loglik']), lik=ashr.lik_pois(y=x, scale=s, link='identity'), mixcompdist='halfuniform', mixsd=pd.Series(np.geomspace(lam.min() + 1e-8, lam.max(), 25)), mode=l) llik.append(np.array(fit.rx2('loglik'))[0]) llik = np.array(llik)
Plot the marginal likelihood against the mode.
cm = plt.get_cmap('Dark2') plt.clf() fig, ax = plt.subplots(2, 1, sharex=True) fig.set_size_inches(6, 3) for a in ax: a.plot(grid, llik, lw=1, c='k') for i, (m, l) in enumerate(zip([fit0[0], fit1[0], np.array(fit2.rx2('fitted_g').rx2('a'))[0], mode, grid[np.argmax(llik)]], ['Point', 'ZIG', 'ash', 'Two step', 'Grid'])): a.axvline(x=m, lw=1, c=cm(i), ls=':', label=l) ax[1].legend(frameon=False, bbox_to_anchor=(1, .5), loc='center left') ax[1].set_xlabel('Mode') ax[1].set_ylim(-2009, -2008) for a in ax: a.set_ylabel('Log lik') fig.tight_layout()
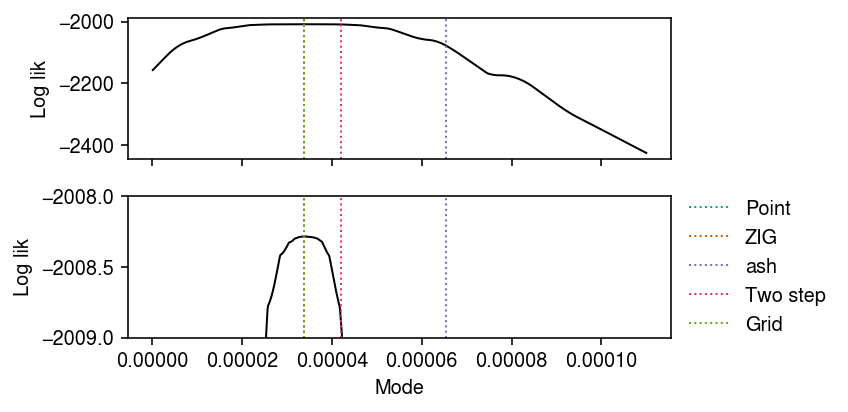
Report the log likelihood of the two step approach.
pd.Series({'pointmass': fit0[-1],
'zig': fit1[-1],
'unimodal': np.array(fit2.rx2('loglik'))[0],
'twostep': np.array(fit3.rx2('loglik'))[0],
})
pointmass -2008.663140 zig -2008.407921 unimodal -2077.552567 twostep -2008.891981 dtype: float64