Mixture of negative binomials

Introduction
Setup
Methods
- EM algorithm
Results
- Simulation
  - Degenerate model

Introduction

Here, we use the EM algorithm to fit a mixture of negative binomials to count data.

The motivating example is explaining bimodal variation in spike-in molecule counts using the fact that the distribution of size factors is bimodal:

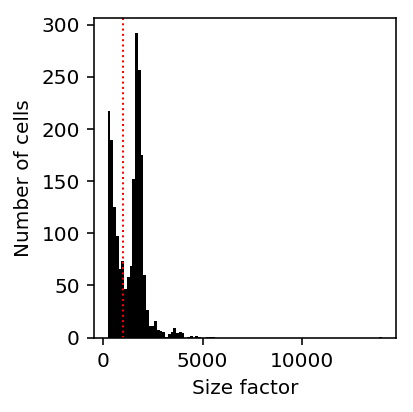
Setup

import numpy as np
import pandas as pd
import scipy.optimize as so
import scipy.stats as st
import scipy.special as sp
import scqtl.simple

%matplotlib inline
%config InlineBackend.figure_formats = set(['retina'])

import matplotlib.pyplot as plt
plt.rcParams['figure.facecolor'] = 'w'

Methods

EM algorithm

The complete data model is:

\[ x_i \mid \lambda_i \sim \mathrm{Poisson}(\lambda_i) \]

\[ \lambda_i \mid z_i \sim \mu_{z_i} \mathrm{Gamma}(\phi_{z_i}^{-1}, \phi_{z_i}^{-1}) \]

def nb_llik(x, mean, inv_disp):
  return (x * np.log(mean / inv_disp + 1e-8) -
          x * np.log1p(mean / inv_disp) -
          inv_disp * np.log1p(mean / inv_disp) +
          sp.gammaln(x + inv_disp) -
          sp.gammaln(inv_disp) -
          sp.gammaln(x + 1))

def objective(theta, x, z):
  # Important: theta gets flattened by minimize
  n_components = z.shape[1]
  mean = np.exp(theta[:n_components])
  inv_disp = np.exp(theta[n_components:])
  return -(np.log(z + 1e-8) + nb_llik(x, mean, inv_disp)).sum()

def check_result(opt):
  return (opt.success and
          np.isfinite(opt.fun) and
          np.isfinite(opt.jac).all())

def init(n_components, x, z):
  theta = np.random.normal(size=(2, n_components))
  for j in range(n_components):
    theta[0,j] = np.log(x[z[:,j] > 0.5].mean())
  return theta

def mstep(theta, x, z):
  n_components = theta.shape[1]
  theta1 = np.zeros(theta.shape)
  x0 = init(n_components, x, z)
  for j in range(n_components):
    mstep = so.minimize(objective, x0=x0[:,j], args=(x, z[:,j]))
    if not check_result(mstep):
      raise RuntimeError('M step failed to converge')
    theta1[:,j] = mstep.x
  return theta1

def mix_nb(x, n_components=2, max_iters=1000, max_retries=10):
  """Fit mixture of negative binomials via EM"""
  x = x.reshape(-1, 1)
  n = x.shape[0]
  z = np.random.uniform(size=(n, n_components))
  z /= z.sum(axis=1, keepdims=True)
  theta = init(n_components, x, z)

  obj = np.inf
  for i in range(max_iters):
    theta1 = mstep(theta, x, z)
    update = np.array([objective(t, x, z) for t in theta1.T]).sum()
    assert np.isfinite(update)
    if update > obj:
      raise RuntimeError('objective decreased')
    elif np.isclose(update, obj):
      print(f'{i}: {obj}')
      return z, theta, obj
    else:
      obj = update
      print(f'{i}: {obj}')
      theta = theta1
      # E step
      z = sp.softmax(nb_llik(x, np.exp(theta[0]), np.exp(theta[1])), axis=1)
  raise RuntimeError('failed to converge')

Results

Simulation

Degenerate model

First, make sure the easy case (one component) works. Generate some Poisson data.

np.random.seed(1)
x = np.random.poisson(lam=100, size=(1000, 1))
z = np.ones((x.shape[0], 1))

theta0 = init(1, x, z)
objective(theta0, x, z)

5430.563796635256

opt = so.minimize(objective, x0=theta0, args=(x, z), method='Nelder-Mead')
assert opt.success
{'fitted': np.exp(opt.x[0]), 'true': 100}

{'fitted': 100.66675997637512, 'true': 100}

Generate some negative binomial data.

np.random.seed(1)
x = st.nbinom(n=3, p=1e-3).rvs(size=(1000, 1))
z = np.ones((x.shape[0], 1))
opt = so.minimize(objective, x0=theta0, args=(x, z), method='Nelder-Mead')
assert opt.success
{'fitted_mean': np.exp(opt.x[0]),
 'true_mean': st.nbinom(n=3, p=1e-3).mean(),
 'fitted_var': np.exp(2 * opt.x[0] - opt.x[1]),
 'true_var': st.nbinom(n=3, p=1e-3).var()}

{'fitted_mean': 2978.7653010814693,
'true_mean': 2997.0,
'fitted_var': 2889291.139179591,
'true_var': 2997000.0}

Now make sure it works when we give the model more than the true number of components.

z = np.zeros((x.shape[0], 2))
z[:,0] = (np.random.uniform(size=z.shape[0]) < 0.5).astype(int)
z[:,1] = 1 - z[:,0]
theta0 = init(2, x, z)
objective(theta0, x, z)

36078.88820426077

opt = so.minimize(objective, x0=theta0, args=(x, z), method='Nelder-Mead')
assert opt.success
opt.x

array([7.99922953, 1.12198022, 1.70447064, 0.38548806])

x[z[:,0].astype(bool)].mean(), np.exp(opt.x[0])

(2994.14859437751, 2978.741830944349)

x[~(z[:,0].astype(bool))].mean(), np.exp(opt.x[2])

(2963.430278884462, 8.322971383121208)