Differential expression based on distribution deconvolution
Table of Contents
Introduction
For gene \(j\), consider the generative model for counts \(x_i, i=1, \ldots, n\):
\[ x_i \mid s_i, \lambda_i \sim \mathrm{Pois}(s_i \lambda_i) \]
\[ \lambda_i \sim g_{z_i}(\cdot) \]
where \(z_i\) denotes group membership. How do we use this model to test for differential expression?
Joyce Hsiao reports that commonly used count-based methods (deSeq2, edgeR) do not successfully control Type 1 error. But our preliminary results show a relatively simple count-based approach adequately controls Type 1 error here. There are two possible reasons:
- We are comparing much larger groups
- We are not shrinking dispersion parameters across genes
Setup
import numpy as np import pandas as pd import rpy2.robjects.packages import rpy2.robjects.pandas2ri import scipy.optimize as so import scipy.stats as st import scmodes import scqtl.simple mass = rpy2.robjects.packages.importr('MASS') rpy2.robjects.pandas2ri.activate()
%matplotlib inline %config InlineBackend.figure_formats = set(['retina'])
import matplotlib.pyplot as plt plt.rcParams['figure.facecolor'] = 'w'
Methods
Deconvolution-based test
In the simplest case, suppose \(g_k = \delta_{\mu_k}\). Then,
\[ \hat\mu_k = \frac{\sum_i [z_i = k] x_i}{\sum_i [z_i = k] s_i} \]
This suggests a simple likelihood ratio test, comparing the null model
\[ x_i \sim \mathrm{Pois}(s_i \mu_0) \]
against an alternative model:
\[ x_i \sim \mathrm{Pois}(s_i \mu_{z_i}) \]
More generally, we can compare the null model:
\[ x_i \sim \mathrm{Pois}(s_i \lambda_i) \]
\[ \lambda_i \sim g_0(\cdot) \]
against an alternative model:
\[ x_i \sim \mathrm{Pois}(s_i \lambda_i) \]
\[ \lambda_i \sim g_{z_i}(\cdot) \]
In the general case, it will not be true that \(-2 \ln(l_0 - l_1) \sim \chi^2_1\). However, for the case where \(g\) is assumed to be Gamma distributed, it will be \(\chi^2_1\) or \(\chi^2_2\), depending on whether we allow dispersions to vary across groups also.
Realistic null simulation
Take a real homogeneous data set (sorted cells from Zheng et al. 2017), and randomly partition samples into two groups.
cd8 = scmodes.dataset.read_10x('/project2/mstephens/aksarkar/projects/singlecell-ideas/data/10xgenomics/cytotoxic_t/filtered_matrices_mex/hg19/', return_df=True) s = cd8.sum(axis=1)
np.random.seed(0)
z = np.random.uniform(size=cd8.shape[0]) < 0.5
z.mean()
0.5071015770398668
Results
Point-mass deconvolution
First look at an idealized case where log-transform fails.
np.random.seed(0) N = 100 onehot = np.zeros((2 * N, 2)) onehot[:N, 0] = 1 onehot[N:, 1] = 1 s = onehot.dot(np.array([1e5, 2e5])) mu = 1e-5 llrs = [] pvals = [] for trial in range(1000): x = np.random.poisson(lam=s * mu) mu0 = x.sum() / s.sum() mu1 = x[:N].sum() / s[:N].sum() mu2 = x[N:].sum() / s[N:].sum() llr = st.poisson(mu=mu0).logpmf(x).sum() - st.poisson(mu=onehot.dot(np.array([mu1, mu2]))).logpmf(x).sum() llrs.append(llr) llrs = np.array(llrs)
Look at the QQ plot.
plt.clf() plt.gcf().set_size_inches(3, 3) plt.scatter(st.chi2(1).ppf(np.linspace(0, 1, llrs.shape[0])), np.sort(-2 * llrs), c='k', s=2) plt.plot([0, 11], [0, 11], c='r', lw=1, ls=':') plt.xlabel('Expected chi-square') plt.ylabel('Observed chi-square')
Text(0, 0.5, 'Observed chi-square')
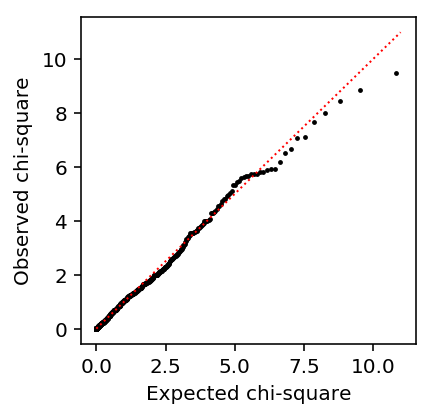
Look at the histogram of p-values.
plt.clf() plt.gcf().set_size_inches(3, 3) plt.hist(st.chi2(1).sf(-2 * llrs), np.linspace(0, 1, 11), density=True, color='black') plt.axhline(y=1, lw=1, ls=':', c='r') plt.xlabel('P-value') plt.ylabel('Density') plt.tight_layout()
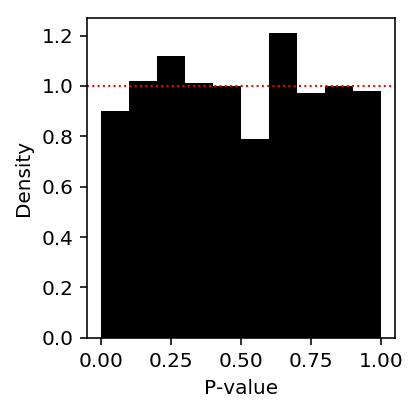
Deconvolve gene expression assuming \(g\) is a point mass (counts are marginally Poisson distributed). Naively, this should work because the data are informative about the mean.
def de(x, s, z): """Return LRT p-value x - counts (n,) s - size factors (n,) z - boolean group assignment (n,) """ mu0 = x.sum() / s.sum() mu1 = x[z].sum() / s[z].sum() mu2 = x[~z].sum() / s[~z].sum() onehot = pd.get_dummies(z) llr = st.poisson(mu=mu0).logpmf(x).sum() - st.poisson(mu=onehot.dot(np.array([mu2, mu1]))).logpmf(x).sum() assert llr < 0 return pd.Series({'mu0': mu0, 'mu1': mu1, 'mu2': mu2, 'llr': llr, 'p': st.chi2(1).sf(-2 * llr)})
de_res = cd8.apply(de, axis=0, args=(s, z)).T
plt.clf() plt.gcf().set_size_inches(3, 3) plt.hist(de_res.loc[:,'p'], np.linspace(0, 1, 11), density=True, color='black') plt.axhline(y=1, lw=1, ls=':', c='r') plt.xlabel('P-value') plt.ylabel('Density') plt.tight_layout()
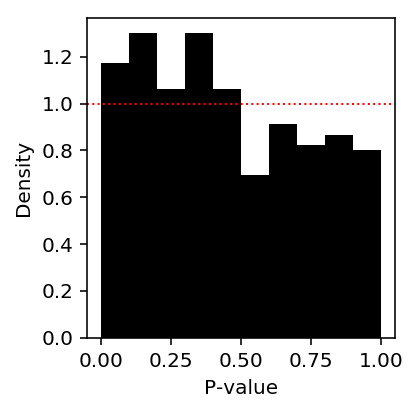
This result suggests that the sampling variance is not correctly estimated.
Gamma deconvolution
Deconvolve gene expression assuming group-specific Gammas under the alternative.
def fit_nb_collapse(x, s): """Return NB or Poisson solution, whichever is more sensible""" try: res = scqtl.simple.fit_nb(x, s) except: # Failure to converge res = scqtl.simple.fit_pois(x, s) # Converged to solution with large inverse overdispersion, so log likelihood # is nonsense if res[-1] > 0: res = scqtl.simple.fit_pois(x, s) return res def de_nb(x, s, z): """Return LRT p-value x - counts (n,) s - size factors (n,) z - boolean group assignment (n,) """ res0 = fit_nb_collapse(x, s) res1 = fit_nb_collapse(x[z], s[z]) res2 = fit_nb_collapse(x[~z], s[~z]) llr = res0[-1] - (res1[-1] + res2[-1]) return pd.Series({'mu0': res0[0], 'mu1': res1[0], 'mu2': res2[0], 'llr': llr, 'p': st.chi2(2).sf(-2 * llr)})
de_nb_res = cd8.sample(n=100, axis=1, random_state=1).apply(de_nb, axis=0, args=(s, z)).T
Look at the histogram of p-values.
plt.clf() plt.gcf().set_size_inches(3, 3) plt.hist(de_nb_res['p'], np.linspace(0, 1, 11), density=True, color='black') plt.axhline(y=1, lw=1, ls=':', c='r') plt.xlabel('P-value') plt.ylabel('Density') plt.tight_layout()
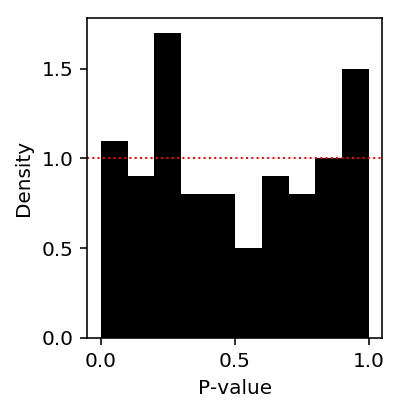
Look at the QQ plot.
plt.clf() plt.gcf().set_size_inches(3, 3) plt.scatter(st.chi2(2).ppf(np.linspace(0, 1, de_nb_res.shape[0])), np.sort(-2 * de_nb_res['llr']), c='k', s=2) plt.plot([0, 11], [0, 11], c='r', lw=1, ls=':') plt.xlabel('Expected chi-square') plt.ylabel('Observed chi-square')
Text(0, 0.5, 'Observed chi-square')
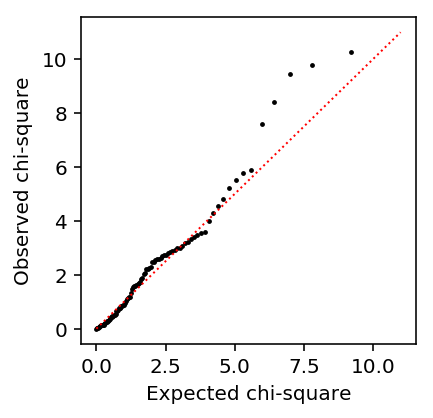
NB GLM
The Gamma deconvolution approach above corresponds to a generalized linear model:
\[ x_i \sim \mathrm{NB}(\mu_i, \phi_{z_i}) \]
\[ \ln(\mu_i) = \mathbf{z}_i + \ln s_i \]
where \(\mathrm{NB}(\mu, \phi)\) denotes the negative binomial distribution with mean \(\mu\) and variance \(\mu^2\phi\) and \(\mathbf{z}_i\) denotes a one-hot vector representing the group membership.
This level of flexibility in the dispersion parameters isn't readily available in existing GLM implementations. However, it is not obvious this level of flexibility is actually required.
If we consider the Gamma deconvolution approach essentially a \(t\)-test (mean and variance per group), we can compare the GLM approach with a single dispersion parameter \(\phi\) to a \(t\)-test with pooled variance.
def de_glm(x, s, z): f = rpy2.robjects.Formula('x ~ z + offset(log(s))') f.environment['x'] = x f.environment['z'] = pd.Series(z.astype(int)) f.environment['s'] = s res = mass.glm_nb(f) pval = np.array(rpy2.robjects.r['coef'](rpy2.robjects.r['summary'](res)))[1,-1] return pval
de_glm_res = cd8.sample(n=100, axis=1, random_state=1).apply(de_glm, axis=0, args=(s, z)).T
Look at the histogram of p-values.
plt.clf() plt.gcf().set_size_inches(3, 3) plt.hist(de_glm_res, np.linspace(0, 1, 11), density=True, color='black') plt.axhline(y=1, lw=1, ls=':', c='r') plt.xlabel('P-value') plt.ylabel('Density') plt.tight_layout()
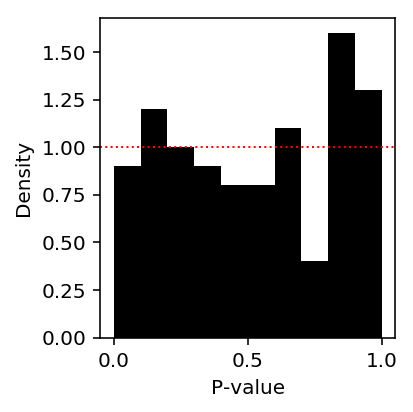
Debugging NB GLM
Figure out what happened in the DSC.
library(dplyr) res = dscrutils::dscquery("/project2/mstephens/aksarkar/projects/dsc-log-fold-change/dsc/benchmark", targets=c("data_poisthin.prop_null", "data_poisthin.nsamp", "type1error"), verbose=FALSE) out = plyr::ddply(res, c("data_poisthin.prop_null", "data_poisthin.nsamp", "type1error.output.file"), function (x) {readRDS(sprintf("/project2/mstephens/aksarkar/projects/dsc-log-fold-change/dsc/benchmark/%s.rds", x$type1error.output.file))$type_one_error}) out %>% group_by(data_poisthin.nsamp, data_poisthin.prop_null) %>% summarise(mean(V1), sd(V1))
| 100 | 0.9 | 0.0233333333333333 | 0.0114155814869796 |
| 100 | 1 | 0.0235 | 0.0104163333279998 |
| 500 | 0.9 | 0.0448888888888889 | 0.00838379781743461 |
| 500 | 1 | 0.0426 | 0.00783439709089205 |
head(out)
| 0.9 | 100 | type1error/datapoisthin1glmnb1type1error1 | 0.0133333333333333 |
| 0.9 | 100 | type1error/datapoisthin13glmnb2type1error2 | 0.0333333333333333 |
| 0.9 | 100 | type1error/datapoisthin17glmnb2type1error2 | 0.0244444444444444 |
| 0.9 | 100 | type1error/datapoisthin21glmnb2type1error2 | 0.0166666666666667 |
| 0.9 | 100 | type1error/datapoisthin25glmnb2type1error2 | 0.0244444444444444 |
| 0.9 | 100 | type1error/datapoisthin29glmnb2type1error2 | 0.05 |
Look at a false positive.
dat = readRDS("/project2/mstephens/aksarkar/projects/dsc-log-fold-change/dsc/benchmark/data_poisthin/data_poisthin_29.rds") glm_res = readRDS("/project2/mstephens/aksarkar/projects/dsc-log-fold-change/dsc/benchmark/glm_nb/data_poisthin_29_glm_nb_2.rds") parsed = data.frame(beta=dat$beta, betahat=glm_res$log_fold_change_est, shat=glm_res$s_hat, p=glm_res$pval)
y = dat$Y[10,] s = colSums(dat$Y) z = dat$X[,2] fit = MASS::glm.nb(y ~ z + offset(log(s))) summary(fit)
Call:
MASS::glm.nb(formula = y ~ z + offset(log(s)), init.theta = 0.3319585934,
link = log)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.0912 -0.8465 -0.5935 -0.0329 3.6257
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -7.6827 0.2914 -26.360 < 2e-16 ***
z -1.2983 0.4794 -2.708 0.00676 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for Negative Binomial(0.332) family taken to be 1)
Null deviance: 70.030 on 99 degrees of freedom
Residual deviance: 62.383 on 98 degrees of freedom
AIC: 184.42
Number of Fisher Scoring iterations: 1
Theta: 0.332
Std. Err.: 0.105
2 x log-likelihood: -178.425
Can we fix this by fitting group-specific dispersions?
dat = rpy2.robjects.r['readRDS']('/project2/mstephens/aksarkar/projects/dsc-log-fold-change/dsc/benchmark/data_poisthin/data_poisthin_29.rds')
X = np.array(dat.rx2('Y')).T x = X[:,9] s = X.sum(axis=1) z = np.zeros(100).astype(bool) z[:50] = 1
de_nb(x, s, z)
mu0 0.000292 mu1 0.000167 mu2 0.000404 llr -4.349299 p 0.012916 dtype: float64
Look at this gene.
plt.clf() fig, ax = plt.subplots(2, 1) fig.set_size_inches(6, 4) ax[0].hist(x[z], bins=np.arange(x.max() + 1), color='k', alpha=0.6, label='Group 1') ax[0].hist(x[~z], bins=np.arange(x.max() + 1), color='r', alpha=0.6, label='Group 2') ax[0].legend(frameon=False) ax[0].set_xlabel('Num mols') ax[0].set_ylabel('Num cells') for c, k in zip(plt.get_cmap('Dark2').colors, ['Gamma', 'ZIG', 'Unimodal', 'ZIEF', 'NPMLE']): ax[1].plot(*getattr(scmodes.deconvolve, f'fit_{k.lower()}')(x, s), color=c, lw=1, label=k) ax[1].set_xlabel('Latent gene expression') ax[1].set_ylabel('CDF') ax[1].legend(frameon=False) fig.tight_layout()
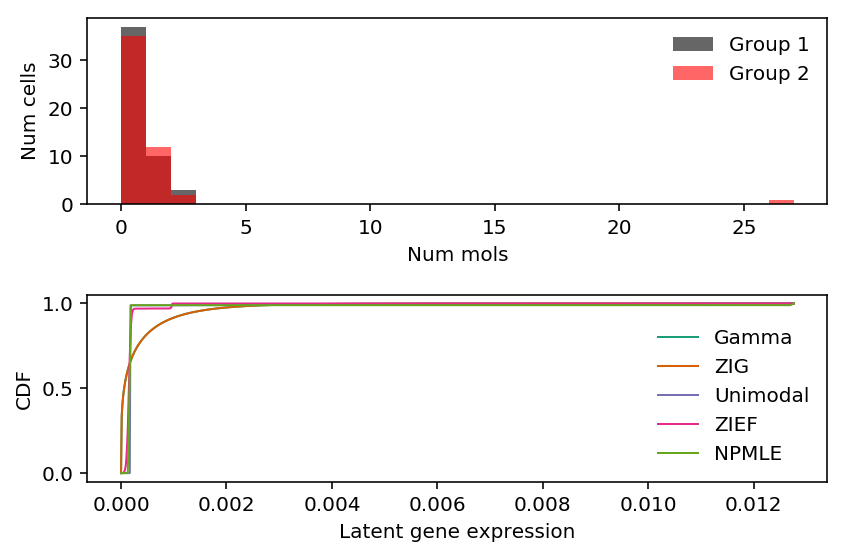
Correct null model for Gamma deconvolution DE
Above we compared \(M_0\):
\[ x_i \mid s_i, \lambda_i \sim \mathrm{Poisson}(s_i \lambda_i) \]
\[ \lambda_i \mid \cdot \sim \mathrm{Gamma}(\mu_0, \phi_0) \]
to \(M_1\):
\[ x_i \mid s_i, \lambda_i \sim \mathrm{Poisson}(s_i \lambda_i) \]
\[ \lambda_i \mid \cdot \sim \mathrm{Gamma}(\mu_{z_i}, \phi_{z_i}) \]
However, this model comparison tests something more than just differential expression: \(M_1\) will fit the data better even if \(\mu_1 = \mu_2\), but \(\phi_1 \neq \phi_2\).
We really need to test \(\mu_1 \neq \mu_2\), allowing \(\phi_1 \neq \phi_2\). In principle, this could be achieved by computing a \(t\)-statistic; however, the necessary variance (standard error) is difficult to estimate.
Instead, we could test \(M_1\) against \(M'_0\):
\[ x_i \mid s_i, \lambda_i \sim \mathrm{Poisson}(s_i \lambda_i) \]
\[ \lambda_i \mid \cdot \sim \mathrm{Gamma}(\mu_0, \phi_{z_i}) \]
def nb_null_obj(theta, x, s, Z): mean = np.exp(theta[0]) inv_disp = Z.dot(np.exp(theta[1:])) return -st.nbinom(n=inv_disp, p=1 / (1 + s * mean / inv_disp)).logpmf(x).sum() def fit_nb_null(x, s, z): x, s = scqtl.simple.check_args(x, s) Z = pd.get_dummies(z).values opt = so.minimize(nb_null_obj, x0=[np.log(x.sum() / s.sum()), 10, 10], args=(x, s, Z), method='Nelder-Mead') if not opt.success: raise RuntimeError(opt.message) mean = np.exp(opt.x[0]) inv_disp0 = np.exp(opt.x[1]) inv_disp1 = np.exp(opt.x[2]) nll = opt.fun return mean, inv_disp0, inv_disp1, -nll def de_nb2(x, s, z): """Return LRT p-value x - counts (n,) s - size factors (n,) z - boolean group assignment (n,) """ res0 = fit_nb_null(x, s, z) res1 = fit_nb_collapse(x[z], s[z]) res2 = fit_nb_collapse(x[~z], s[~z]) llr = res0[-1] - (res1[-1] + res2[-1]) return pd.Series({'mu0': res0[0], 'inv_disp01': res0[1], 'inv_disp02': res0[2], 'mu1': res1[0], 'inv_disp1': res1[1], 'mu2': res2[0], 'inv_disp2': res2[1], 'llr': llr, 'p': st.chi2(2).sf(-2 * llr)})
Try on an example.
dat = rpy2.robjects.r['readRDS']('/project2/mstephens/aksarkar/projects/dsc-log-fold-change/dsc/benchmark/data_poisthin/data_poisthin_29.rds')
X = np.array(dat.rx2('Y')).T x = X[:,9] s = X.sum(axis=1) z = np.zeros(100).astype(bool) z[:50] = 1
res = fit_nb_null(x, s, z)
res
(0.0002303843030721306, 0.17676454746805434, 2.057596627861452, -90.55969515068075)
de_nb2(x, s, z)
mu0 0.000230 inv_disp01 0.176765 inv_disp02 2.057597 mu1 0.000167 inv_disp1 4.781742 mu2 0.000404 inv_disp2 0.204504 llr -2.118471 p 0.120215 dtype: float64