Deep unsupervised clustering of scRNA-seq data
Table of Contents
Introduction
Two major strategies for clustering scRNA-seq data are:
- Building a \(k\)-nearest neighbor graph on the data, and applying a community detection algorithm (e.g., Blondel et al. 2008, Traag et al. 2018)
- Fitting a topic model to the data (e.g., Dey et al. 2017, Gonzáles-Blas et al. 2019)
The main disadvantage of strategy (1) is that, as commonly applied to transformed counts, it does not separate measurement error and biological variation of interest (Sarkar and Stephens 2021). The main disadvantage of strategy (2) is that it does not account for transcriptional noise (Raj 2008). We previously developed a simple mixture model that could address the second issue. Here, we develop an alternative method based on GMVAE, which allows us to explore a different way of separating and representing transcriptional noise.
Setup
import anndata import mpebpm import numpy as np import pandas as pd import scanpy as sc import scipy.stats as st import sklearn.decomposition as skd import sklearn.mixture as skm import torch import torch.utils.data as td import torch.utils.tensorboard as tb import torchvision import umap
%matplotlib inline %config InlineBackend.figure_formats = set(['retina'])
import colorcet import matplotlib.pyplot as plt plt.rcParams['figure.facecolor'] = 'w' plt.rcParams['font.family'] = 'Nimbus Sans'
Methods
Gaussian VAE
In perhaps the simplest case, one assumes \( \DeclareMathOperator\Bern{Bernoulli} \DeclareMathOperator\E{E} \DeclareMathOperator\KL{\mathcal{KL}} \DeclareMathOperator\Gam{Gamma} \DeclareMathOperator\Mult{Multinomial} \DeclareMathOperator\N{\mathcal{N}} \DeclareMathOperator\Pois{Poisson} \DeclareMathOperator\diag{diag} \DeclareMathOperator\KL{\mathcal{KL}} \newcommand\kl[2]{\KL(#1\;\Vert\;#2)} \newcommand\xiplus{x_{i+}} \newcommand\mi{\mathbf{I}} \newcommand\va{\mathbf{a}} \newcommand\vb{\mathbf{b}} \newcommand\vm{\mathbf{m}} \newcommand\vs{\mathbf{s}} \newcommand\vu{\mathbf{u}} \newcommand\vx{\mathbf{x}} \newcommand\vy{\mathbf{y}} \newcommand\vz{\mathbf{z}} \newcommand\vlambda{\boldsymbol{\lambda}} \newcommand\vmu{\boldsymbol{\mu}} \newcommand\vphi{\boldsymbol{\phi}} \newcommand\vpi{\boldsymbol{\pi}} \)
\begin{align} \vx_i \mid \vz_i, s^2 &\sim \N(f(\vz_i), s^2 \mi)\\ \vz_i \mid s_0^2 &\sim \N(0, s_0^2 \mi), \end{align}where
- \(\vx_i\) denotes a \(p\)-dimensional observation
- \(\vz_i\) denotes the \(d\)-dimensional latent variable corresponding to observation \(\vx_i\), with \(d \ll p\)
- \(f\) is a (fully connected, say) neural network mapping latent variables to the (noiseless, true) mean vector
Remark This is slightly different than the original presentation of VAEs (Kingma and Welling 2014).
There are two inference tasks: (1) estimating \(s^2, s_0^2, f\) and (2) estimating \(p(\vz_i \mid \vx_i, s^2, s_0^2, f)\). This is an instance of variational empirical Bayes (Wang et al. 2020), which is typically done by introducing a variational approximation parameterized by an inference network (Gershman and Goodman 2014).
\begin{equation} q(\vz_i \mid \vx_i) = \N(\mu(\vz_i), \diag(\sigma^2(\vz_i))), \end{equation}where \(\mu, \sigma^2\) are neural networks mapping the latent variable \(\vz_i\) to the mean and diagonal of the covariance matrix of the approximate posterior distribution.
Remark The inference network is not strictly necessary.
class FC(torch.nn.Module): """Fully connected layers""" def __init__(self, input_dim, hidden_dim=128): super().__init__() self.net = torch.nn.Sequential( torch.nn.Linear(input_dim, hidden_dim), torch.nn.ReLU(), # torch.nn.BatchNorm1d(hidden_dim), torch.nn.Linear(hidden_dim, hidden_dim), torch.nn.ReLU(), # torch.nn.BatchNorm1d(hidden_dim), ) def forward(self, x): return self.net(x) class DeepGaussian(torch.nn.Module): """Gaussian distribution parameterized by FC networks for mean and (diagonal) scale""" def __init__(self, input_dim, output_dim, hidden_dim=128): super().__init__() self.net = FC(input_dim, hidden_dim) self.mean = torch.nn.Linear(hidden_dim, output_dim) self.scale = torch.nn.Sequential( torch.nn.Linear(hidden_dim, output_dim), torch.nn.Softplus()) def forward(self, x): q = self.net(x) return self.mean(q), self.scale(q) + 1e-3 class DeepCategorical(torch.nn.Module): """Categorical distribution parameterized by FC network for logits""" def __init__(self, input_dim, output_dim, hidden_dim=128): super().__init__() self.net = FC(input_dim, hidden_dim) self.probs = torch.nn.Sequential( torch.nn.Linear(hidden_dim, output_dim), torch.nn.Softmax(dim=1)) def forward(self, x): q = self.net(x) return self.probs(q)
Then, the ELBO
\begin{equation} \ell = \sum_i \E_q[\ln p(\vz_i \mid \vz_i)] - \KL(q(\vz_i \mid \vx_i) \Vert p(\vz_i)), \end{equation}where the second term is analytic (since it is the KL divergence between two Gaussians). In practice, one replaces the intractable first term \(\E_q[\ln p(\vz_i \mid \vz_i)]\) with a Monte Carlo integral, where samples from \(q\) are simulated from a standard distribution transformed by some differentiable function \(g\) (Kingma and Welling 2014). Then, it is trivial to generalize this setup to other likelihoods.
class VAE(torch.nn.Module): def __init__(self, input_dim, latent_dim, hidden_dim=128): super().__init__() self.residual_scale_raw = torch.nn.Parameter(torch.zeros([1])) self.prior_scale_raw = torch.nn.Parameter(torch.zeros([1])) self.encoder = DeepGaussian(input_dim, latent_dim, hidden_dim) self.decoder = torch.nn.Sequential( FC(latent_dim, hidden_dim), torch.nn.Linear(hidden_dim, input_dim)) def forward(self, x, n_samples, writer=None, global_step=None): softplus = torch.nn.functional.softplus z_mean, z_scale = self.encoder.forward(x) qz = torch.distributions.Normal(z_mean, z_scale) kl = torch.distributions.kl.kl_divergence(qz, torch.distributions.Normal(0., softplus(self.prior_scale_raw))).sum(dim=1) z = qz.rsample(n_samples) x_mean = self.decoder.forward(z) err = torch.distributions.Normal(x_mean, softplus(self.residual_scale_raw)).log_prob(x).mean(dim=0).sum(dim=1) loss = -(err - kl).sum() if writer is not None: writer.add_scalar('loss/kl', kl.sum(), global_step) writer.add_scalar('loss/neg_err', -err.sum(), global_step) writer.add_scalar('loss/neg_elbo', loss, global_step) return loss def fit(self, data, n_epochs, n_samples=1, log_dir=None, **kwargs): assert torch.cuda.is_available() self.cuda() n_samples = torch.Size([n_samples]) if log_dir is not None: writer = tb.SummaryWriter(log_dir) else: writer = None opt = torch.optim.Adam(self.parameters(), **kwargs) global_step = 0 for epoch in range(n_epochs): for (x,) in data: x = x.cuda() opt.zero_grad() loss = self.forward(x, n_samples, writer=writer, global_step=global_step) if torch.isnan(loss): raise RuntimeError('nan loss') loss.backward() opt.step() global_step += 1 return self @torch.no_grad() def residual_scale(self): return torch.nn.functional.softplus(self.residual_scale_raw).cpu().numpy() @torch.no_grad() def prior_scale(self): return torch.nn.functional.softplus(self.prior_scale_raw).cpu().numpy() @torch.no_grad() def get_latent(self, data): zhat = [] for (x,) in data: zhat.append(self.encoder.forward(x)[0].cpu().numpy()) return np.vstack(zhat) @torch.no_grad() def predict(self, data): xhat = [] for (x,) in data: xhat.append(self.decoder.forward(self.encoder.forward(x)[0]).cpu().numpy()) return np.vstack(xhat)
Gaussian mixture prior VAE
Now assume (Kingma et al. 2014, Shu 2016, Dilokthanakul et al. 2016, Jiang et al. 2017)
\begin{align} \vx_i \mid \vz_i, s^2 &\sim \N(f(\vz_i), s^2 \mi)\\ \vz_i \mid \vy_i &\sim \N(\vm_{\vy_i}, \vs_{\vy_i}^2)\\ \vy_i \mid \va &\sim \Mult(1, \va), \end{align}where
- \(\vy_i\) is a one-hot \(k\)-vector denoting the latent cluster assignment
- \(\va\) is the \(k\)-vector of prior probabilities for each cluster assignment
- \(\vm, \vs^2\) are prior means and diagonal covariances for the clusters
Under this model, the marginal prior \(p(\vz_i)\) is a mixture of Gaussians. To perform inference, introduce a variational approximation
\begin{align} q(\vy_i, \vz_i \mid \vx_i) &= q(\vy_i \mid \vx_i)\, q(\vz_i \mid \vx_i, \vy_i)\\ q(\vy_i \mid \vx_i) &= \Mult(1, \pi(\vx_i))\\ q(\vz_i \mid \vx_i, \vy_i) &= \N(\mu(\vx_i, \vy_i), \sigma^2(\vx_i, \vy_i)), \end{align}where
- \(\pi(\cdot)\) is a fully-connected neural network mapping observations to latent labels (more precisely, posterior probabilities)
- \(\mu(\cdot), \sigma^2(\cdot)\) are fully-connected neural networks mapping observations and latent labels to latent variables
Importantly, the approximate posterior distribution of latent variables is Gaussian, not a mixture of Gaussians. The ELBO
\begin{equation} \ell = \sum_i \E_q\left[\ln p(\vx_i \mid \vz_i) + \ln\frac{p(\vy_i)}{q(\vy_i \mid \vx_i)} + \ln\frac{p(\vz_i \mid \vy_i)}{q(\vz_i \mid \vx_i, \vy_i)}\right], \end{equation}in which the expectation over \(q(\vy_i \mid \vx_i)\) is computed exactly (by summing over mixture components) and the expectation over \(q(\vz_i \mid \vx_i, \vy_i)\) is replaced by a Monte Carlo integral as above.
class GMVAE(torch.nn.Module): def __init__(self, input_dim, latent_dim, n_clusters, hidden_dim=128): super().__init__() self.n_clusters = n_clusters self.residual_scale_raw = torch.nn.Parameter(torch.zeros([1])) self.encoder_y = DeepCategorical(input_dim, n_clusters, hidden_dim) self.encoder_z = DeepGaussian(input_dim + n_clusters, latent_dim, hidden_dim) self.prior_mean = torch.nn.Parameter(torch.randn([n_clusters, latent_dim])) self.prior_scale_raw = torch.nn.Parameter(torch.randn([n_clusters, latent_dim])) self.decoder_x = torch.nn.Sequential( FC(latent_dim, hidden_dim), torch.nn.Linear(hidden_dim, input_dim)) def forward(self, x, n_samples, labels=None, writer=None, global_step=None, eps=1e-16): softplus = torch.nn.functional.softplus # [batch_size, n_clusters] probs = self.encoder_y.forward(x) # Important: accumulate negative ELBO loss = (probs * (torch.log(probs + eps) + torch.log(torch.tensor(self.n_clusters, dtype=torch.float)))).sum() assert not torch.isnan(loss) if writer is not None and labels is not None: # labels is one-hot [batch_size, n_clusters] with torch.no_grad(): if labels.shape[1] == 2: writer.add_scalar('loss/cross_entropy_p', torch.nn.functional.binary_cross_entropy(probs, labels), global_step) writer.add_scalar('loss/cross_entropy_1p', torch.nn.functional.binary_cross_entropy(1 - probs, labels), global_step) writer.add_scalar('loss/cond_entropy', -(probs * torch.log(probs + eps)).mean(), global_step) y = torch.eye(self.n_clusters).cuda() # Important: really marginalize over y for k in range(self.n_clusters): z_mean, z_scale = self.encoder_z.forward(torch.cat([x, y[k].repeat(x.shape[0], 1)], dim=1)) # [batch_size, latent_dim] qz = torch.distributions.Normal(z_mean, z_scale).rsample(n_samples) loss += (probs[:,k].reshape(-1, 1) * (torch.distributions.Normal(z_mean, z_scale).log_prob(qz) - torch.distributions.Normal(self.prior_mean[k], softplus(self.prior_scale_raw[k])).log_prob(qz))).mean(dim=0).sum() assert not torch.isnan(loss) # [batch_size, input_dim] x_mean = self.decoder_x.forward(qz) loss -= (probs[:,k].reshape(-1, 1) * torch.distributions.Normal(x_mean, softplus(self.residual_scale_raw)).log_prob(x)).mean(dim=0).sum() assert not torch.isnan(loss) assert loss > 0 if writer is not None: writer.add_scalar('loss/neg_elbo', loss, global_step) return loss def fit(self, data, n_samples, n_epochs=100, log_dir=None, **kwargs): assert torch.cuda.is_available() self.cuda() n_samples = torch.Size([n_samples]) if log_dir is not None: writer = tb.SummaryWriter(log_dir) else: writer = None opt = torch.optim.Adam(self.parameters(), **kwargs) global_step = 0 for epoch in range(n_epochs): for batch in data: x = batch.pop(0).cuda() if batch: y = batch.pop(0).cuda() opt.zero_grad() loss = self.forward(x, n_samples, labels=y, writer=writer, global_step=global_step) if torch.isnan(loss): raise RuntimeError('nan loss') loss.backward() opt.step() global_step += 1 return self @property @torch.no_grad() def residual_scale(self): return torch.nn.functional.softplus(self.residual_scale_raw).cpu().numpy() @property @torch.no_grad() def prior_scale(self): return torch.nn.functional.softplus(self.prior_scale_raw).cpu().numpy() @torch.no_grad() def get_labels(self, data): yhat = [] for x, *_ in data: yhat.append(self.encoder_y.forward(x).cpu().numpy()) return np.vstack(yhat) @torch.no_grad() def get_latent(self, data): zhat = [] y = torch.eye(self.n_clusters).cuda() for x, *_ in data: yhat = self.encoder_y.forward(x) zhat.append(torch.stack([yhat[:,k].reshape(-1, 1) * self.encoder_z.forward(torch.cat([x, y[k].repeat(x.shape[0], 1)], dim=1))[0] for k in range(self.n_clusters)]).sum(dim=0).cpu().numpy()) return np.vstack(zhat) @torch.no_grad() def predict(self, data): xhat = [] y = torch.eye(self.n_clusters).cuda() for x, *_ in data: yhat = self.encoder_y.forward(x) zhat = torch.stack([yhat[:,k].reshape(-1, 1) * self.encoder_z.forward(torch.cat([x, y[k].repeat(x.shape[0], 1)], dim=1))[0] for k in range(self.n_clusters)]).sum(dim=0) xhat.append(self.decoder_x(zhat).cpu().numpy()) return np.vstack(xhat)
Bernoulli GMVAE
Implement the approach for the Bernoulli likelihood, to model MNIST.
\begin{equation} x_{ij} \mid \vz_i \sim \Bern((f(\vz_i))_j), \end{equation}where \(x_{ij}\) is a binary pixel.
class BGMVAE(torch.nn.Module): """GMVAE with Bernoulli likelihood""" def __init__(self, input_dim, latent_dim, n_clusters, hidden_dim=128): super().__init__() self.n_clusters = n_clusters self.encoder_y = DeepCategorical(input_dim, n_clusters, hidden_dim) self.encoder_z = DeepGaussian(input_dim + n_clusters, latent_dim, hidden_dim) self.decoder_z = DeepGaussian(n_clusters, latent_dim, hidden_dim) self.decoder_x = torch.nn.Sequential( FC(latent_dim + n_clusters, hidden_dim), torch.nn.Linear(hidden_dim, input_dim), torch.nn.Sigmoid() ) def forward(self, x, n_samples, labels=None, writer=None, global_step=None): # [batch_size, n_clusters] probs = self.encoder_y.forward(x) # Important: Negative ELBO loss = (probs * (torch.log(probs + 1e-16) + torch.log(torch.tensor(self.n_clusters, dtype=torch.float)))).sum() assert not torch.isnan(loss) if writer is not None and labels is not None: with torch.no_grad(): cond_entropy = -(probs * torch.log(probs + 1e-16)).sum(dim=1).mean() writer.add_scalar('loss/cond_entropy', cond_entropy, global_step) yhat = torch.zeros(x.shape[0], dtype=torch.long, device='cuda') for k in range(labels.shape[1]): query = torch.argmax(probs, dim=1) == k if query.any(): yhat[query] = torch.argmax(labels[query].sum(dim=0)) writer.add_scalar('loss/accuracy', (yhat == torch.argmax(labels, dim=1)).sum() / x.shape[0], global_step) # Assume cuda y = torch.eye(self.n_clusters).cuda() # [n_clusters, latent_dim] prior_mean, prior_scale = self.decoder_z.forward(y) for k in range(self.n_clusters): mean, scale = self.encoder_z.forward(torch.cat([x, y[k].repeat(x.shape[0], 1)], dim=1)) # [n_samples, batch_size, latent_dim] qz = torch.distributions.Normal(mean, scale).rsample(n_samples) loss += (probs[:,k].reshape(-1, 1) * (torch.distributions.Normal(mean, scale).log_prob(qz) - torch.distributions.Normal(prior_mean[k], prior_scale[k]).log_prob(qz))).mean(dim=0).sum() assert not torch.isnan(loss) # [n_samples, batch_size, input_dim + n_clusters] px = self.decoder_x(torch.cat([qz, y[k].repeat(1, x.shape[0], 1)], dim=2)) loss -= (probs[:,k].reshape(-1, 1) * (x * torch.log(px + 1e-16) + (1 - x) * torch.log(1 - px + 1e-16))).mean(dim=0).sum() assert not torch.isnan(loss) assert loss > 0 if writer is not None: writer.add_scalar('loss/neg_elbo', loss, global_step) return loss def fit(self, data, n_samples=1, n_epochs=100, log_dir=None, **kwargs): self.cuda() n_samples = torch.Size([n_samples]) if log_dir is not None: writer = tb.SummaryWriter(log_dir) else: writer = None opt = torch.optim.Adam(self.parameters(), **kwargs) global_step = 0 for epoch in range(n_epochs): for x, y in data: # TODO: put entire MNIST on GPU in advance x = x.cuda() y = y.cuda() opt.zero_grad() loss = self.forward(x, n_samples, labels=y, writer=writer, global_step=global_step) if torch.isnan(loss): raise RuntimeError('nan loss') loss.backward() opt.step() global_step += 1 return self @torch.no_grad() def get_labels(self, data): yhat = [] for x, *_ in data: x = x.cuda() yhat.append(torch.nn.functional.softmax(fit.encoder_y.forward(x), dim=1).cpu().numpy()) return np.vstack(yhat) @torch.no_grad() def get_latent(self, data): zhat = [] y = torch.eye(self.n_clusters).cuda() for x, *_ in data: x = x.cuda() yhat = torch.nn.functional.softmax(self.encoder_y.forward(x), dim=1) zhat.append(torch.stack([yhat[:,k].reshape(-1, 1) * fit.encoder_z.forward(torch.cat([x, y[k].repeat(x.shape[0], 1)], dim=1))[0] for k in range(fit.n_clusters)]).sum(dim=0).cpu().numpy()) return np.vstack(zhat)
For reference, implement Kingma et al. M2 model.
class M2(torch.nn.Module): def __init__(self, input_dim, latent_dim, n_clusters, hidden_dim=128): super().__init__() self.n_clusters = n_clusters self.encoder_y = DeepCategorical(input_dim, n_clusters, hidden_dim) self.encoder_z = DeepGaussian(input_dim + n_clusters, latent_dim, hidden_dim) self.decoder_x = torch.nn.Sequential( FC(latent_dim + n_clusters, hidden_dim), torch.nn.Linear(hidden_dim, input_dim), torch.nn.Sigmoid() ) def forward(self, x, n_samples, labels=None, writer=None, global_step=None): # [batch_size, n_clusters] probs = self.encoder_y.forward(x) # Important: Negative ELBO loss = (probs * (torch.log(probs + 1e-16) + torch.log(torch.tensor(self.n_clusters, dtype=torch.float)))).sum() assert not torch.isnan(loss) if writer is not None and labels is not None: with torch.no_grad(): cond_entropy = -(probs * torch.log(probs + 1e-16)).sum(dim=1).mean() writer.add_scalar('loss/cond_entropy', cond_entropy, global_step) yhat = torch.zeros(x.shape[0], dtype=torch.long, device='cuda') for k in range(labels.shape[1]): query = torch.argmax(probs, dim=1) == k if query.any(): yhat[query] = torch.argmax(labels[query].sum(dim=0)) writer.add_scalar('loss/accuracy', (yhat == torch.argmax(labels, dim=1)).sum() / x.shape[0], global_step) # Assume cuda y = torch.eye(self.n_clusters).cuda() for k in range(self.n_clusters): mean, scale = self.encoder_z.forward(torch.cat([x, y[k].repeat(x.shape[0], 1)], dim=1)) # [n_samples, batch_size, latent_dim] qz = torch.distributions.Normal(mean, scale).rsample(n_samples) loss += (probs[:,k].reshape(-1, 1) * (torch.distributions.Normal(mean, scale).log_prob(qz) - torch.distributions.Normal(0., 1.).log_prob(qz))).sum() assert not torch.isnan(loss) # [n_samples, batch_size, input_dim + num_clusters] px = self.decoder_x(torch.cat([qz, y[k].repeat(1, x.shape[0], 1)], dim=2)) loss -= (probs[:,k].reshape(-1, 1) * (x * torch.log(px + 1e-16) + (1 - x) * torch.log(1 - px + 1e-16))).mean(dim=0).sum() assert not torch.isnan(loss) assert loss > 0 if writer is not None: writer.add_scalar('loss/neg_elbo', loss, global_step) return loss def fit(self, data, n_samples=1, n_epochs=100, log_dir=None, **kwargs): self.cuda() n_samples = torch.Size([n_samples]) if log_dir is not None: writer = tb.SummaryWriter(log_dir) else: writer = None opt = torch.optim.Adam(self.parameters(), **kwargs) global_step = 0 for epoch in range(n_epochs): for x, y in data: # TODO: put entire MNIST on GPU in advance x = x.cuda() y = y.cuda() opt.zero_grad() loss = self.forward(x, n_samples, labels=y, writer=writer, global_step=global_step) if torch.isnan(loss): raise RuntimeError('nan loss') loss.backward() opt.step() global_step += 1 return self @torch.no_grad() def get_labels(self, data): yhat = [] for x, *_ in data: x = x.cuda() yhat.append(self.encoder_y.forward(x).cpu().numpy()) return np.vstack(yhat) @torch.no_grad() def get_latent(self, data): zhat = [] y = torch.eye(self.n_clusters).cuda() for x, *_ in data: x = x.cuda() yhat = self.encoder_y.forward(x) zhat.append(torch.stack([yhat[:,k].reshape(-1, 1) * self.encoder_z.forward(torch.cat([x, y[k].repeat(x.shape[0], 1)], dim=1))[0] for k in range(self.n_clusters)]).sum(dim=0).cpu().numpy()) return np.vstack(zhat)
Poisson GMVAE
Now implement the case we are interested in for scRNA-seq data, with Poisson measurement model (likelihood)
\begin{equation} \vx_i \mid \xiplus, \vz_i \sim \Pois(\xiplus (f(\vz_i))_j) \end{equation}where
- \(x_{ij}\) denotes the number of molecules of gene \(j = 1, \ldots, p\) observed in cell \(i = 1, \ldots, n\)
- \(\xiplus \triangleq \sum_j x_{ij}\) denotes the total number of molecules observed in cell \(i\)
class PGMVAE(torch.nn.Module): def __init__(self, input_dim, latent_dim, n_clusters, hidden_dim=128): super().__init__() self.n_clusters = n_clusters self.encoder_y = DeepCategorical(input_dim, n_clusters, hidden_dim) self.encoder_z = DeepGaussian(input_dim + n_clusters, latent_dim, hidden_dim) self.decoder_z = DeepGaussian(n_clusters, latent_dim, hidden_dim) self.decoder_x = torch.nn.Sequential( FC(latent_dim, hidden_dim), torch.nn.Linear(hidden_dim, input_dim), torch.nn.Softplus() ) def forward(self, x, s, labels=None, writer=None, global_step=None): # [batch_size, n_clusters] logits = self.encoder_y.forward(x) probs = torch.nn.functional.softmax(logits, dim=1) # Important: Negative ELBO loss = (probs * (torch.log(probs + 1e-16) + torch.log(torch.tensor(self.n_clusters, dtype=torch.float)))).sum() assert not torch.isnan(loss) if writer is not None and labels is not None: with torch.no_grad(): writer.add_scalar('loss/cross_entropy', min(torch.nn.functional.binary_cross_entropy(probs, labels), torch.nn.functional.binary_cross_entropy(1 - probs, labels)), global_step) writer.add_scalar('loss/cond_entropy', -(probs * torch.log(probs + 1e-16)).mean(), global_step) # Assume cuda y = torch.eye(self.n_clusters).cuda() # [n_clusters, latent_dim] prior_mean, prior_scale = self.decoder_z.forward(y) for k in range(self.n_clusters): mean, scale = self.encoder_z.forward(torch.cat([x, y[k].repeat(x.shape[0], 1)], dim=1)) # [batch_size, latent_dim] # TODO: n_samples > 1 breaks BatchNorm in decoder qz = torch.distributions.Normal(mean, scale).rsample() loss += (probs[:,k].reshape(-1, 1) * (torch.distributions.Normal(mean, scale).log_prob(qz) - torch.distributions.Normal(prior_mean[k], prior_scale[k]).log_prob(qz))).sum() assert not torch.isnan(loss) # [batch_size, input_dim] lam = self.decoder_x(qz) loss -= (probs[:,k].reshape(-1, 1) * (x * torch.log(s * lam) - s * lam - torch.lgamma(x + 1))).sum() assert not torch.isnan(loss) assert loss > 0 if writer is not None: writer.add_scalar('loss/neg_elbo', loss, global_step) return loss def fit(self, data, n_epochs=100, log_dir=None, **kwargs): self.cuda() if log_dir is not None: writer = tb.SummaryWriter(log_dir) opt = torch.optim.Adam(self.parameters(), **kwargs) global_step = 0 for epoch in range(n_epochs): for batch in data: assert len(batch) == 3 x = batch.pop(0) s = batch.pop(0) if batch: y = batch.pop(0) else: y = None opt.zero_grad() loss = self.forward(x, s, labels=y, writer=writer, global_step=global_step) if torch.isnan(loss): raise RuntimeError('nan loss') loss.backward() opt.step() global_step += 1 return self @torch.no_grad() def get_labels(self, data): yhat = [] for x, *_ in data: yhat.append(torch.nn.functional.softmax(self.encoder_y.forward(x), dim=1).cpu().numpy()) return np.vstack(yhat) @torch.no_grad() def get_latent(self, data): zhat = [] y = torch.eye(self.n_clusters).cuda() for x, *_ in data: yhat = torch.nn.functional.softmax(self.encoder_y.forward(x), dim=1) zhat.append(torch.stack([yhat[:,k].reshape(-1, 1) * self.encoder_z.forward(torch.cat([x, y[k].repeat(x.shape[0], 1)], dim=1))[0] for k in range(fit.n_clusters)]).sum(dim=0).cpu().numpy()) return np.vstack(zhat)
Results
GMM sanity check
As a sanity check, simulate from a mixture of 5 Gaussians convolved with Gaussian noise.
num_obs = 10000 num_features = 10 num_clusters = 5 noise_scale = 0.5 rng = np.random.default_rng(1) mu = rng.normal(size=(num_clusters, num_features)) sigma = rng.lognormal(size=(num_clusters, num_features)) y = rng.choice(num_clusters, size=num_obs) Y = pd.get_dummies(y).values x = rng.normal(loc=mu[y], scale=noise_scale + sigma[y])
Plot a UMAP of the data.
u = umap.UMAP().fit_transform(x)
cm = plt.get_cmap('Dark2') plt.clf() plt.gcf().set_size_inches(3.5, 3) for k in range(num_clusters): plt.scatter(u[y == k,0], u[y == k,1], s=1, alpha=0.1, color=cm(k), label=f'C{k}') plt.gca().set_aspect('equal', adjustable='datalim') l = plt.legend(frameon=False, markerscale=4, handletextpad=0, loc='center left', bbox_to_anchor=(1, .5)) for h in l.legendHandles: h.set_alpha(1) plt.xlabel('UMAP 1') plt.ylabel('UMAP 2') plt.tight_layout()
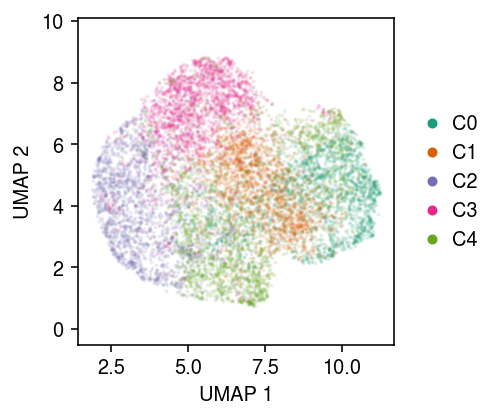
Report the oracle log likelihood.
st.norm(loc=mu[y], scale=noise_scale + sigma[y]).logpdf(x).sum()
-182471.79127489863
GMM on observed data
Fit a GMM with the oracle number of clusters.
m0 = skm.GaussianMixture(n_components=num_clusters).fit(x)
Report the clustering accuracy.
yhat = m0.predict(x) acc = 0 for k in range(num_clusters): idx = np.argmax(pd.get_dummies(y)[yhat == k].sum(axis=0)) acc += (y[yhat == k] == idx).sum() acc /= y.shape[0] acc
0.858
Report the log likelihood, marginalizing over \(p(\vy \mid \vx)\).
yhat = m0.predict_proba(x) np.log(np.stack([yhat[:,k] * st.multivariate_normal(mean=m0.means_[k], cov=m0.covariances_[k]).pdf(x) for k in range(num_clusters)]).sum(axis=0)).sum()
-181326.07982124935
VAE followed by GMM
Fit a Gaussian VAE to the data.
run = 6 latent_dim = 4 batch_size = 32 lr = 1e-2 n_samples = 10 n_epochs = 20 torch.manual_seed(run) data = td.DataLoader(td.TensorDataset(torch.tensor(x, dtype=torch.float, device='cuda')), batch_size=batch_size, drop_last=True, shuffle=True) m2 = VAE(input_dim=num_features, latent_dim=latent_dim) m2.fit(data, n_epochs=n_epochs, n_samples=n_samples, lr=lr) data = td.DataLoader(td.TensorDataset(torch.tensor(x, dtype=torch.float, device='cuda')), batch_size=batch_size) zhat = m2.get_latent(data) xhat = m2.predict(data)
Compare the predicted values to the observed values.
plt.clf() plt.gcf().set_size_inches(3, 3) plt.scatter(x.ravel(), xhat.ravel(), s=1, alpha=0.1, c='k') plt.gca().set_aspect('equal', adjustable='datalim') plt.xlabel('Observed value') plt.ylabel('Predicted value') plt.tight_layout()
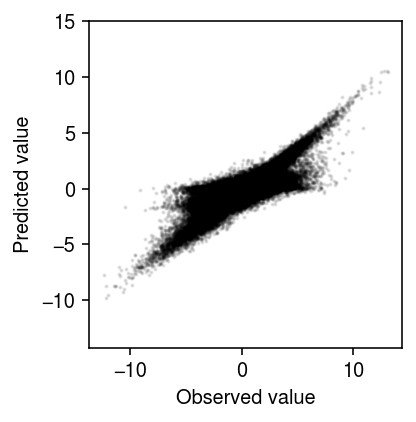
Plot UMAP of the embedding.
u = umap.UMAP(random_state=1).fit_transform(zhat)
cm = plt.get_cmap('Dark2') plt.clf() plt.gcf().set_size_inches(3.5, 3) for k in range(num_clusters): plt.scatter(u[y == k,0], u[y == k,1], s=1, alpha=0.1, color=cm(k), label=f'C{k}') plt.gca().set_aspect('equal', adjustable='datalim') l = plt.legend(frameon=False, markerscale=4, handletextpad=0, loc='center left', bbox_to_anchor=(1, .5)) for h in l.legendHandles: h.set_alpha(1) plt.xlabel('UMAP 1') plt.ylabel('UMAP 2') plt.tight_layout()
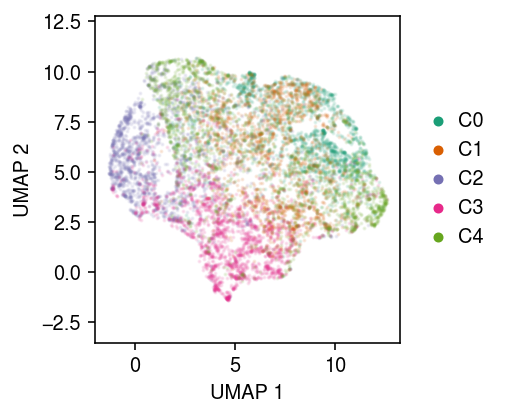
Fit a GMM in the embedding space, then report the clustering accuracy.
m2_gmm = skm.GaussianMixture(n_components=num_clusters).fit(zhat) yhat = m2_gmm.predict(zhat) acc = 0 for k in range(num_clusters): idx = np.argmax(pd.get_dummies(y)[yhat == k].sum(axis=0)) acc += (y[yhat == k] == idx).sum() acc /= y.shape[0] acc
0.5425
GMVAE
Now, fit GMVAE to the data, fixing to the oracle number of clusters.
run = 2 latent_dim = 4 batch_size = 32 lr = 1e-2 n_samples = 10 n_epochs = 20 torch.manual_seed(run) data = td.DataLoader(td.TensorDataset(torch.tensor(x, dtype=torch.float, device='cuda'), torch.tensor(Y, dtype=torch.float, device='cuda')), batch_size=batch_size, drop_last=True, shuffle=True) m3 = GMVAE(input_dim=num_features, n_clusters=num_clusters, latent_dim=latent_dim) m3.fit(data, n_epochs=n_epochs, n_samples=n_samples, lr=lr, log_dir=f'runs/pgmvae/gmm-ex-gmvae-{run}-{lr:.1g}-{n_samples}-{batch_size}-{n_epochs}') data = td.DataLoader(td.TensorDataset(torch.tensor(x, dtype=torch.float, device='cuda'), torch.tensor(Y, dtype=torch.float, device='cuda')), batch_size=batch_size) zhat = m3.get_latent(data) yhat = np.argmax(m3.get_labels(data), axis=1) xhat = m3.predict(data)
Compare the predicted values to the observed values.
plt.clf() plt.gcf().set_size_inches(3, 3) plt.scatter(x.ravel(), xhat.ravel(), s=1, alpha=0.1, c='k') plt.gca().set_aspect('equal', adjustable='datalim') plt.xlabel('Observed value') plt.ylabel('Predicted value') plt.tight_layout()
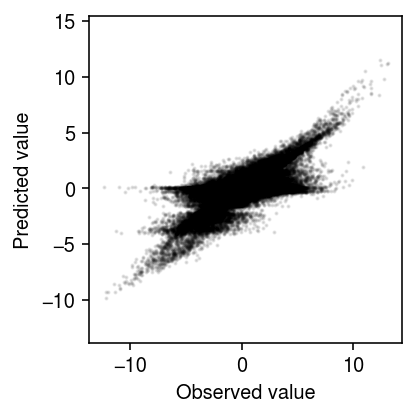
Plot UMAP of the embedding.
u = umap.UMAP(random_state=1).fit_transform(zhat)
cm = plt.get_cmap('Dark2') plt.clf() fig, ax = plt.subplots(1, 2) fig.set_size_inches(6, 3) for k in range(num_clusters): ax[0].scatter(u[y == k,0], u[y == k,1], s=1, alpha=0.1, color=cm(k), label=f'C{k}') ax[1].scatter(u[yhat == k,0], u[yhat == k,1], s=1, alpha=0.1, color=cm(k), label=f'C{k}') for a in ax: a.set_aspect('equal', adjustable='datalim') a.set_xlabel('UMAP 1') ax[0].set_title('True labels') ax[1].set_title('Predicted labels') l = ax[1].legend(frameon=False, markerscale=4, handletextpad=0, loc='center left', bbox_to_anchor=(1, .5)) for h in l.legendHandles: h.set_alpha(1) ax[0].set_ylabel('UMAP 2') fig.tight_layout()
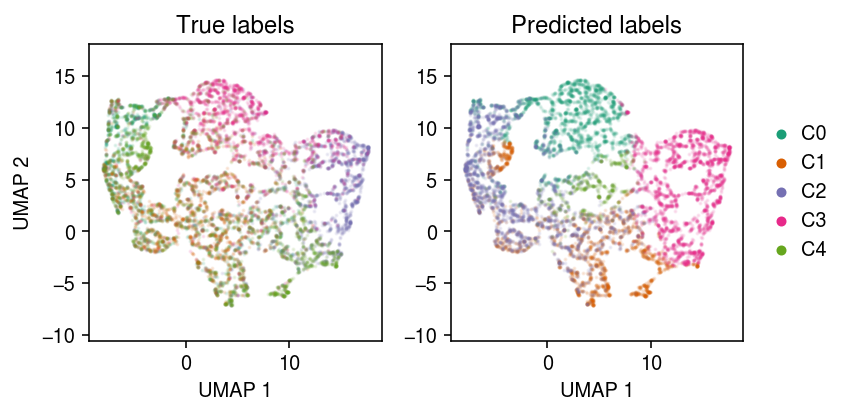
Report the clustering accuracy.
acc = 0 for k in range(num_clusters): idx = np.argmax(pd.get_dummies(y)[yhat == k].sum(axis=0)) acc += (y[yhat == k] == idx).sum() acc /= y.shape[0] acc
0.5156
MNIST sanity check
Replicate Rui Shu’s results, modeling grayscale images of handwritten digits as binarized, flattened pixel vectors. Assume
\begin{align} x_{ij} \mid \vz_i &\sim \Bern((r(\vz_i))_j)\\ \vz_i \mid y_i &\sim \N(m(y_i), s^2(y_i))\\ y_i \mid \va &\sim \Mult(1, \va), \end{align}where \(r\) is a fully-connected neural network mapping latent variables to pixel probabilities.
batch_size = 32 mnist_data = torchvision.datasets.MNIST( root='/scratch/midway2/aksarkar/singlecell/', transform=lambda x: (np.frombuffer(x.tobytes(), dtype='uint8') > 0).astype(np.float32), target_transform=lambda x: np.eye(10)[x]) data = td.DataLoader(mnist_data, batch_size=batch_size, shuffle=True, pin_memory=True)
First, fit Kingma et al. M2 model.
K = 10 lr = 5e-3 n_epochs = 2 n_samples = 1 latent_dim = 10 M2_fits = dict() for seed in range(5): torch.manual_seed(seed) M2_fits[seed] = (M2(input_dim=mnist_data[0][0].shape[0], latent_dim=latent_dim, n_clusters=K) .fit(data, lr=lr, n_samples=n_samples, n_epochs=n_epochs, log_dir=f'runs/m2/mnist-{latent_dim}-{K}-{seed}-{lr:.1g}-{batch_size}-{n_samples}-{n_epochs}'))
Now fit BGMVAE.
K = 10 lr = 5e-3 n_epochs = 2 latent_dim = 10 bgmvae_fits = dict() for seed in range(5): torch.manual_seed(seed) bgmvae_fits[seed] = (BGMVAE(input_dim=mnist_data[0][0].shape[0], latent_dim=latent_dim, n_clusters=K) .fit(data, lr=lr, n_samples=1, n_epochs=n_epochs, log_dir=f'runs/bgmvae/mnist-{latent_dim}-{seed}-{lr:.1g}-{batch_size}-{n_epochs}-{K}') )
Get the approximate posterior distribution on labels.
data = td.DataLoader(mnist_data, batch_size=batch_size, shuffle=False, pin_memory=True) yhat = fit.get_labels(data)
Assign labels to the estimated clusters using the most frequently occurring ground truth label, then assess clustering accuracy.
acc = 0 for k in range(y.shape[1]): query = np.argmax(y, axis=1) == k idx = np.argmax(yhat[query].sum(axis=0)) acc += (np.argmax(yhat[query], axis=1) == idx).sum() print(k, idx) acc / y.shape[0]
0.6509666666666667
Two-way example
Read sorted immune cell scRNA-seq data (Zheng et al. 2017).
dat = anndata.read_h5ad('/scratch/midway2/aksarkar/singlecell/mix4.h5ad')
We previously applied the standard methodology.
mix2 = dat[dat.obs['cell_type'].isin(['cytotoxic_t', 'b_cells'])] sc.pp.filter_genes(mix2, min_counts=1) sc.pp.pca(mix2, zero_center=False) sc.pp.neighbors(mix2) sc.tl.leiden(mix2) sc.tl.umap(mix2) mix2
AnnData object with n_obs × n_vars = 20294 × 17808 obs: 'barcode', 'cell_type', 'leiden' var: 'ensg', 'name', 'n_cells', 'n_counts' uns: 'leiden', 'neighbors', 'pca', 'umap' obsm: 'X_pca', 'X_umap' varm: 'PCs' obsp: 'connectivities', 'distances'
Fit PGMVAE.
assert torch.cuda.is_available() batch_size = 32 x = mix2.X y = pd.get_dummies(mix2.obs['cell_type'], sparse=True).sparse.to_coo().tocsr() sparse_data = mpebpm.sparse.SparseDataset( mpebpm.sparse.CSRTensor(x.data, x.indices, x.indptr, x.shape, dtype=torch.float).cuda(), torch.tensor(x.sum(axis=1), dtype=torch.float).cuda(), mpebpm.sparse.CSRTensor(y.data, y.indices, y.indptr, y.shape, dtype=torch.float).cuda(), ) collate_fn = getattr(sparse_data, 'collate_fn', td.dataloader.default_collate) data = td.DataLoader(sparse_data, batch_size=batch_size, shuffle=True, collate_fn=collate_fn)
k = 2 seed = 3 lr = 5e-3 n_epochs = 2 latent_dim = 4 torch.manual_seed(seed) fit = (PGMVAE(input_dim=mix2.shape[1], latent_dim=latent_dim, n_clusters=k) .fit(data, lr=lr, n_epochs=n_epochs, log_dir=f'runs/pgmvae/mix2-{latent_dim}-{k}-{seed}-{lr:.1g}-{batch_size}-{n_epochs}') )
Get the approximate posterior labels.
data = td.DataLoader(sparse_data, batch_size=batch_size, shuffle=False, collate_fn=collate_fn) yhat = fit.get_labels(data) mix2.obs['comp'] = np.argmax(yhat, axis=1)
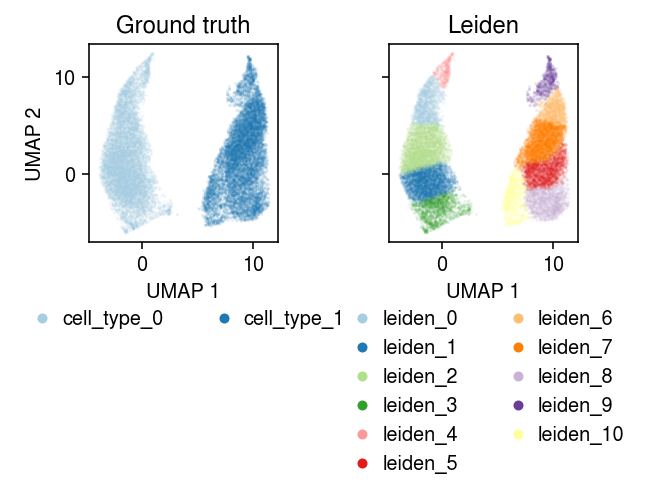
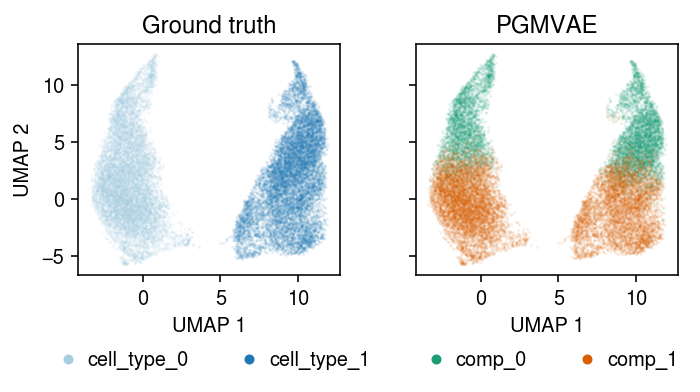
Plot the result.
plt.clf() fig, ax = plt.subplots(1, 2, sharex=True, sharey=True) fig.set_size_inches(5, 3) for a, k, t, cm in zip(ax, ['cell_type', 'comp'], ['Ground truth', 'PGMVAE'], ['Paired', 'Dark2']): for i, c in enumerate(mix2.obs[k].unique()): a.plot(*mix2[mix2.obs[k] == c].obsm["X_umap"].T, c=plt.get_cmap(cm)(i), marker='.', ms=1, lw=0, alpha=0.1, label=f'{k}_{i}') leg = a.legend(frameon=False, markerscale=8, handletextpad=0, loc='upper center', bbox_to_anchor=(.5, -.25), ncol=2) for h in leg.legendHandles: h._legmarker.set_alpha(1) a.set_xlabel('UMAP 1') a.set_title(t) ax[0].set_ylabel('UMAP 2') fig.tight_layout()
Get the latent representation.
zhat = fit.get_latent(data)
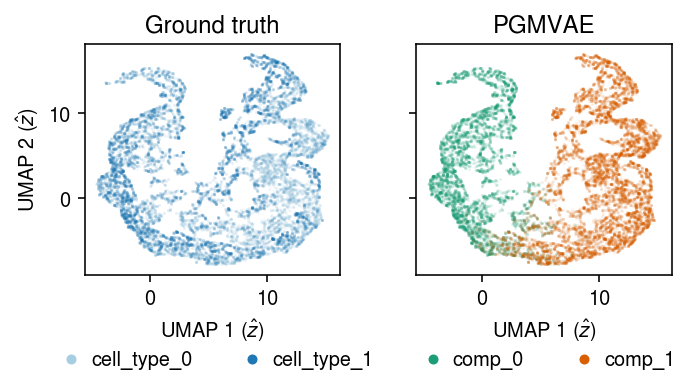
Plot a UMAP of the learned representation.
u = umap.UMAP(n_neighbors=5, n_components=2, metric='euclidean').fit_transform(zhat)
plt.clf() fig, ax = plt.subplots(1, 2, sharex=True, sharey=True) fig.set_size_inches(5, 3) for a, k, t, cm in zip(ax, ['cell_type', 'comp'], ['Ground truth', 'PGMVAE'], ['Paired', 'Dark2']): for i, c in enumerate(mix2.obs[k].unique()): a.plot(*u[mix2.obs[k] == c].T, c=plt.get_cmap(cm)(i), marker='.', ms=1, lw=0, alpha=0.1, label=f'{k}_{i}') leg = a.legend(frameon=False, markerscale=8, handletextpad=0, loc='upper center', bbox_to_anchor=(.5, -.25), ncol=2) for h in leg.legendHandles: h._legmarker.set_alpha(1) a.set_xlabel('UMAP 1 ($\hat{z}$)') a.set_title(t) ax[0].set_ylabel('UMAP 2 ($\hat{z}$)') fig.tight_layout()
Related work
scVI (Lopez et al. 2018, Xu et al. 2020) implements a deep unsupervised (more precisely, semi-supervised) clustering model (Kingma et al. 2014, Dilokthanakul et al. 2016).
\begin{align} x_{ij} \mid s_i, \lambda_{ij} &\sim \Pois(s_i \lambda_{ij})\\ \ln s_i &\sim \N(\cdot)\\ \lambda_{ij} \mid \vz_i &\sim \Gam(\phi_j^{-1}, (\mu_{\lambda}(\vz_i))_j^{-1} \phi_j^{-1})\\ \vz_i \mid y_i, \vu_i &\sim \N(\mu_z(\vu_i, y_i), \diag(\sigma^2(\vu_i, y_i)))\\ y_i \mid \vpi &\sim \Mult(1, \vpi)\\ \vu_i &\sim \N(0, \mi). \end{align}where
- \(y_i\) denotes the cluster assignment for cell \(i\)
- \(\mu_z(\cdot), \sigma^2(\cdot)\) are neural networks mapping the latent cluster variable \(y_i\) and Gaussian noise \(\vu_i\) to the latent variable \(\vz_i\)
- \(\mu_{\lambda}(\cdot)\) is a neural network mapping latent variable \(\vz_i\) to latent gene expression \(\vlambda_{i}\)
To perform variational inference in this model, Lopez et al. introduce inference networks
\begin{align} q(\vz_i \mid \vx_i) &= \N(\cdot)\\ q(y_i \mid \vz_i) &= \Mult(1, \cdot). \end{align}import scvi.dataset import scvi.inference import scvi.models expr = scvi.dataset.AnnDatasetFromAnnData(temp) m = scvi.models.VAEC(expr.nb_genes, n_batch=0, n_labels=2) train = scvi.inference.UnsupervisedTrainer(m, expr, train_size=1, batch_size=32, show_progbar=False, n_epochs_kl_warmup=100) train.train(n_epochs=1000, lr=1e-2)
post = train.create_posterior(train.model, expr) _, _, label = post.get_latent()
The main difference in our approach is that we do not make an assumption of Gamma perturbations in latent gene expression. Instead, we implicitly assume that transcriptional noise is structured, e.g. through the gene-gene regulatory network, such that it is reasonable to model it in the low dimensional space. This assumption simplifies the model in terms of both inference and implementation.
VADE
Jiang et al. 2017 propose Variational Deep Embedding
\begin{align} \vx_i \mid \vz_i, s^2 &\sim \N(f(\vz_i), s^2 \mi)\\ \vz_i \mid y_i &\sim \N(\vm_{\vy_i}, \vs_{\vy_i}^2 \mi)\\ \vy_i \mid \va &\sim \Mult(1, \va), \end{align}where \(\vm, \vs\) are prior means and diagonal covariances, respectively. Under this model, the marginal prior \(p(\vz_i)\) is a mixture of Gaussians.
Remark We have simplified the likelihood.
GMVAE
This specification combines the prior specification of