Mutual nearest neighbors in topic model space

Introduction
Setup
Methods
- Fast approximate nearest neighbors
- GMVAE
Results

Introduction

Haghverdi et al 2018 introduce a method for batch correction based on identifying mutual nearest neighbors. The key idea of the method is to identify cells which should have “equal gene expression” across batches, and compute correction factors based on the observed differences in gene expression, where “difference” is cosine distance. The key intuition of the method is “Proper removal of the batch effect should result in the formation of…clusters, one for each cell type, where each cluster contains a mixture of cells from both batches.”

Our use of MNN pairs involves three assumptions: (i) there is at least one cell population that is present in both batches, (ii) the batch effect is almost orthogonal to the biological subspace, and (iii) batch effect variation is much smaller than the biological effect variation between different cell types

Here, we first investigate the intuition and assumptions underlying MNN correction using real data with known, estimable batch effects (Sarkar et al. 2019). Then, we investigate using NMF/LDA to estimate true gene expression under the generative model

\begin{align*} x_{ij} \mid s_i, \lambda_{ij} &\sim \operatorname{Poisson}(s_i \lambda_{ij})\\ \lambda_{ij} &= \sum_{k=1}^K l_{ik} f_{jk} \end{align*}

and compare MNN applied to this latent space against previous approaches based on cosine distance on normalized counts, or Euclidean distance in a principal component subspace.

Setup

import anndata
import numpy as np
import pandas as pd
import scanpy as sc
import sklearn.decomposition as skd
import torch
import torch.utils.data as td
import torch.utils.tensorboard as tb

%matplotlib inline
%config InlineBackend.figure_formats = set(['retina'])

import matplotlib.pyplot as plt
plt.rcParams['figure.facecolor'] = 'w'
plt.rcParams['font.family'] = 'Nimbus Sans'

Methods

Fast approximate nearest neighbors

M. Aumüller, E. Bernhardsson, A. Faithfull: ANN-Benchmarks: A Benchmarking Tool for Approximate Nearest Neighbor Algorithms. Information Systems 2019. 10.1016/j.is.2019.02.006 https://github.com/erikbern/ann-benchmarks

GMVAE

GMVAE is a modification of the semi-supervised generative model first presented in Kingma & Welling 2014.

def net(input_dim, hidden_dim):
  """Return fully connected network, ReLU activations, one hidden layer, batch
normalization at each layer

  """
  return torch.nn.Sequential(
    torch.nn.Linear(input_dim, hidden_dim),
    torch.nn.BatchNorm1d(hidden_dim),
    torch.nn.ReLU(),
    torch.nn.Linear(hidden_dim, hidden_dim),
    torch.nn.BatchNorm1d(hidden_dim),
    torch.nn.ReLU(),
  )  

# Distributions parameterized by neural nets, to be used for priors and
# variational approximations.

class Categorical(torch.nn.Module):
  def __init__(self, input_dim, output_dim, hidden_dim=128):
    super().__init__()
    self.net = net(input_dim, hidden_dim)
    self.logits = torch.nn.Linear(hidden_dim, output_dim)

  def forward(self, x):
    h = self.net(x)
    return self.logits(h)

class Gaussian(torch.nn.Module):
  def __init__(self, input_dim, output_dim, hidden_dim=128):
    super().__init__()
    self.net = net(input_dim, hidden_dim)
    self.mean = torch.nn.Linear(hidden_dim, output_dim)
    self.scale = torch.nn.Sequential(torch.nn.Linear(hidden_dim, output_dim), torch.nn.Softplus())

  def forward(self, x):
    h = self.net(x)
    return self.mean(h), self.scale(h)

class Poisson(torch.nn.Module):
  def __init__(self, input_dim, output_dim, hidden_dim=128):
    super().__init__()
    self.net = net(input_dim, hidden_dim)
    self.lam = torch.nn.Sequential(torch.nn.Linear(hidden_dim, output_dim), torch.nn.Softplus())

  def forward(self, x):
    h = self.net(x)
    return self.lam(h)

class PVAE(torch.nn.Module):
  def __init__(self, input_dim, latent_dim, covar_dim, hidden_dim=128):
    super().__init__()
    self.qz = Gaussian(input_dim, latent_dim)
    self.px = Poisson(latent_dim + covar_dim, input_dim)
    self.writer = tb.SummaryWriter()

  def forward(self, s, x, c, n_samples, global_step):
    mean, scale = self.qz.forward(x)
    # [n_samples,]
    kl_z = torch.sum(.5 * (1 - 2 * torch.log(scale) + mean ** 2 + scale ** 2), axis=1)
    self.writer.add_scalar('loss/kl_z', kl_z.sum(), global_step)
    # [n_samples, batch_size, input_dim]
    qz = torch.distributions.Normal(mean, scale).rsample(n_samples)
    # [n_samples, batch_size, input_dim + covar_dim]
    qz = torch.cat([qz, c.unsqueeze(0).expand(qz.shape[0], -1, -1)], dim=-1)
    lam = self.px.forward(qz.reshape([-1, qz.shape[2]])).reshape([qz.shape[0], qz.shape[1], -1])
    s = torch.reshape(s, [1, -1, 1])
    # [n_samples,]
    err = torch.mean(torch.sum(x * torch.log(s * lam) - s * lam + torch.lgamma(x + 1), dim=2), dim=0)
    self.writer.add_scalar('loss/err', err.sum(), global_step)
    loss = -torch.sum(err - kl_z)
    self.writer.add_scalar('loss/elbo', loss, global_step)
    assert not torch.isnan(loss)
    return loss

  def fit(self, data, n_epochs, n_samples=10, **kwargs):
    assert torch.cuda.is_available()
    self.cuda()
    n_samples = torch.Size([n_samples])
    opt = torch.optim.RMSprop(self.parameters(), **kwargs)
    global_step = 0
    for epoch in range(n_epochs):
      for s, x, c in data:
        s = s.cuda()
        x = x.cuda()
        c = c.cuda()
        opt.zero_grad()
        loss = self.forward(s, x, c, n_samples=n_samples, global_step=global_step)
        if torch.isnan(loss):
          raise RuntimeError('nan loss')
        loss.backward()
        opt.step()
        global_step += 1
    return self

  @torch.no_grad()
  def latent(self, data):
    res = []
    for _, x, _ in data:
      res.append(self.qz.forward(x.cuda())[0].cpu().numpy())
    res = np.vstack(res)
    return res

class GMVAE(torch.nn.Module):
  r"""Deep generative model

  x_ij \mid s_i, z_i, c_i ~ Pois(s_i [λ(z_i, c_i)]_j)
  z_i \mid y_i ~ N(μ(y_i), σ^2(y_i))
  y_i ~ Mult(1, 1/m, ..., 1/m)

  q(y_i \mid x_i) = Mult(1, π(y_i))
  q(z_i \mid x_i, y_i) = N(m(x_i, y_i), s^2(x_i, y_i))

  where 

  x_{ij} is molecule count (cell i, gene j)
  s_i is total molecule count (cell i)
  c_i is covariate vector (cell i)
  z_i is latent representation (cell i)
  y_i is latent label (cell i)
  λ is a neural network mapping latent_dim + covar_dim => input_dim
  μ, σ^2 are neural nets mapping label_dim => latent_dim
  π is a neural net mapping input_dim => label_dim
  m, s^2 are neural nets mapping 

  """
  def __init__(self, input_dim, latent_dim, covar_dim, label_dim=0, hidden_dim=128):
    super().__init__()
    if label_dim > 0:
      self.qy = Categorical(input_dim, label_dim)
      self.py = torch.distributions.Categorical(probs=torch.ones(label_dim).cuda())
      self.pz = Gaussian(label_dim, hidden_dim)
    else:
      self.qy = None
      self.py = None
      self.pz = None
    self.qz = Gaussian(input_dim + label_dim, hidden_dim)
    self.px = Poisson(latent_dim + covar_dim, hidden_dim)
    self.writer = tb.SummaryWriter()

  def forward(self, s, x, c, n_samples, global_step):
    if self.qy is not None:
      logits = self.qy.forward(x)
      # [batch_size, label_dim]
      qy = torch.distributions.Categorical(logits=logits)
      kl_y = torch.distributions.kl.kl_divergence(qy, self.py).sum()
      self.writer.add_scalar('loss/kl_y', kl_y, global_step)
      y = torch.nn.functional.one_hot(qy.rsample())
      # [n_samples, batch_size, latent_dim]
      prior_mean, prior_scale = self.pz.forward(qy)
      # [batch_size, latent_dim]
      mean, scale = self.qz.forward(torch.cat([x, y], dim=1))
    else:
      y = torch.empty(0)
      kl_y = 0
      prior_mean = 0
      prior_scale = 1
      mean, scale = self.qz.forward(x)

    # [n_samples, batch_size, latent_dim]
    qz = torch.distributions.Normal(mean, scale).rsample(n_samples)
    # [n_samples,]
    kl_z = torch.sum(.5 * (1 + 2 * torch.log(scale / prior_scale) + ((prior_mean - mean) ** 2 + prior_scale - scale) / scale), axis=1)
    self.writer.add_scalar('loss/kl_z', kl.sum(), global_step)

    # [n_samples, batch_size, input_dim]
    lam = self.px.forward(qz.reshape([-1, qz.shape[2]])).reshape([qz.shape[0], qz.shape[1], -1])
    s = torch.reshape(s, [1, -1, 1])
    # [n_samples,]
    err = torch.mean(torch.sum(x * torch.log(s * lam) - s * lam + torch.lgamma(x + 1), dim=2), dim=0)
    self.writer.add_scalar('loss/err', err.sum(), global_step)
    loss = -torch.sum(err - kl_y - kl_z)
    self.writer.add_scalar('loss/elbo', loss, global_step)
    assert not torch.isnan(loss)
    return loss

  def fit(self, data, n_epochs, n_samples=10, **kwargs):
    assert torch.cuda.is_available()
    self.cuda()
    n_samples = torch.Size([n_samples])
    opt = torch.optim.RMSprop(self.parameters(), **kwargs)
    global_step = 0
    for epoch in range(n_epochs):
      for s, x, c in data:
        s = s.cuda()
        x = x.cuda()
        c = c.cuda()
        opt.zero_grad()
        loss = self.forward(s, x, c, n_samples=n_samples, global_step=global_step)
        if torch.isnan(loss):
          raise RuntimeError('nan loss')
        loss.backward()
        opt.step()
        global_step += 1
    return self

  @torch.no_grad()
  def latent(self, data):
    res = []
    for _, x, _ in data:
      x = x.cuda()
      logits = self.qy.forward(x)
      torch.distributions.Categorical(logits=logits)
      y = torch.nn.functional.one_hot(qy.rsample())
      res.append(self.qz.forward(torch.cat([x, y], dim=1)).cpu().numpy())
    res = np.vstack(res)
    return res

Results

iPSC data

Load the iPSC data.

x = anndata.read_h5ad('/project2/mstephens/aksarkar/projects/singlecell-ideas/data/ipsc/ipsc.h5ad')

Take all cells from batch 1. A priori, there could be clusters by individual and plate.

y = x[x.obs['batch'] == 'b1']

Use the default approach, projecting \(\ln(x+1)\) into a principal component subspace and computing nearest neighbors.

sc.pp.neighbors(y)
sc.tl.umap(y, copy=False)

cm = plt.get_cmap('Paired')
plt.clf()
fig, ax = plt.subplots(1, 2)
fig.set_size_inches(6, 3)
for i, k in enumerate(y.obs['chip_id'].unique()):
  query = y[y.obs['chip_id'] == k].obsm['X_umap']
  ax[0].scatter(query[:,0], query[:,1], s=1, c=cm(i), label=k)
ax[0].set_title('By donor')
for i, k in enumerate(y.obs['experiment'].unique()):
  query = y[y.obs['experiment'] == k].obsm['X_umap']
  ax[1].scatter(query[:,0], query[:,1], s=1, c=cm(i), label=k)
ax[1].set_title('By chip')
for a in ax:
  a.set_xlabel('UMAP 1')
  a.set_ylabel('UMAP 2')
fig.tight_layout()

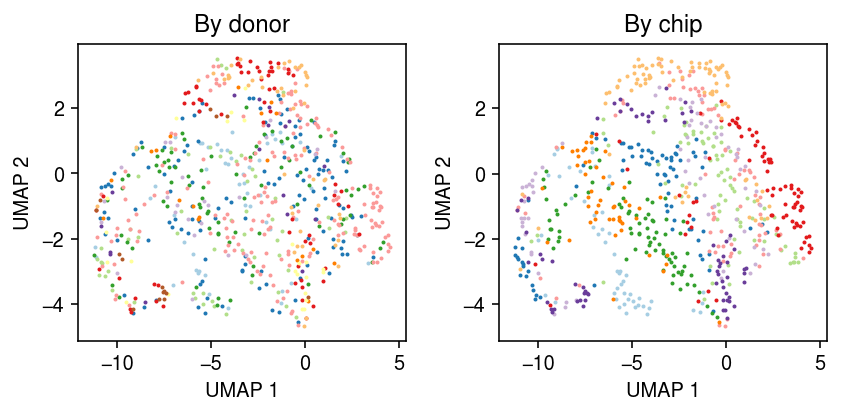
Take all cells from NA18507. A priori, there could be clusters by batch.

y = x[x.obs['chip_id'] == 'NA18507']
sc.pp.neighbors(y)
sc.tl.umap(y, copy=False)

cm = plt.get_cmap('Paired')
plt.clf()
fig, ax = plt.subplots(1, 2)
fig.set_size_inches(6, 3)
for i, k in enumerate(y.obs['batch'].unique()):
  query = y[y.obs['batch'] == k].obsm['X_umap']
  ax[0].scatter(query[:,0], query[:,1], s=1, c=cm(i), label=k)
ax[0].set_title('By batch')
for i, k in enumerate(y.obs['experiment'].unique()):
  query = y[y.obs['experiment'] == k].obsm['X_umap']
  ax[1].scatter(query[:,0], query[:,1], s=1, c=cm(i), label=k)
ax[1].set_title('By chip')
for a in ax:
  a.set_xlabel('UMAP 1')
  a.set_ylabel('UMAP 2')
fig.tight_layout()

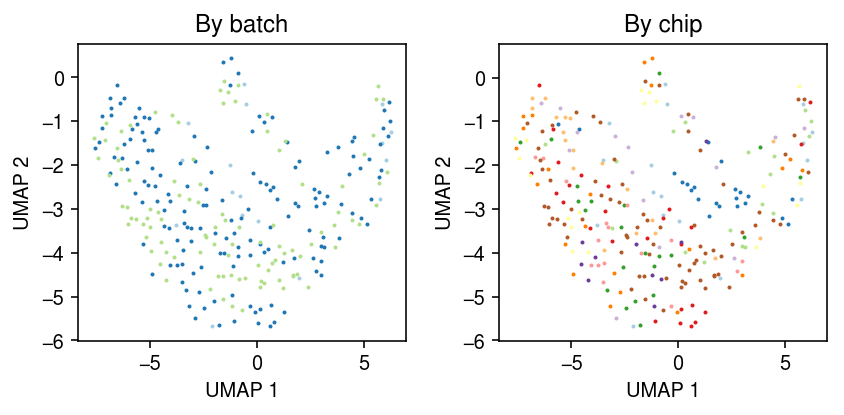
Look at the all cells from all individuals measured in both batches 1 and 2.

ix = set(x.obs.loc[x.obs['batch'] == 'b1','chip_id']) & set(x.obs.loc[x.obs['batch'] == 'b2','chip_id'])
ix

{'NA18507', 'NA18508', 'NA19190'}

y = x[x.obs['chip_id'].isin(ix)]
sc.pp.neighbors(y)
sc.tl.umap(y, copy=False)

cm = plt.get_cmap('Paired')
plt.clf()
fig, ax = plt.subplots(1, 2)
fig.set_size_inches(6, 3)
for i, k in enumerate(y.obs['batch'].unique()):
  query = y[y.obs['batch'] == k].obsm['X_umap']
  ax[0].scatter(query[:,0], query[:,1], s=1, c=cm(i), label=k)
ax[0].set_title('By batch')
for i, k in enumerate(y.obs['chip_id'].unique()):
  query = y[y.obs['chip_id'] == k].obsm['X_umap']
  ax[1].scatter(query[:,0], query[:,1], s=1, c=cm(i), label=k)
ax[1].set_title('By individual')
for a in ax:
  a.set_xlabel('UMAP 1')
  a.set_ylabel('UMAP 2')
fig.tight_layout()

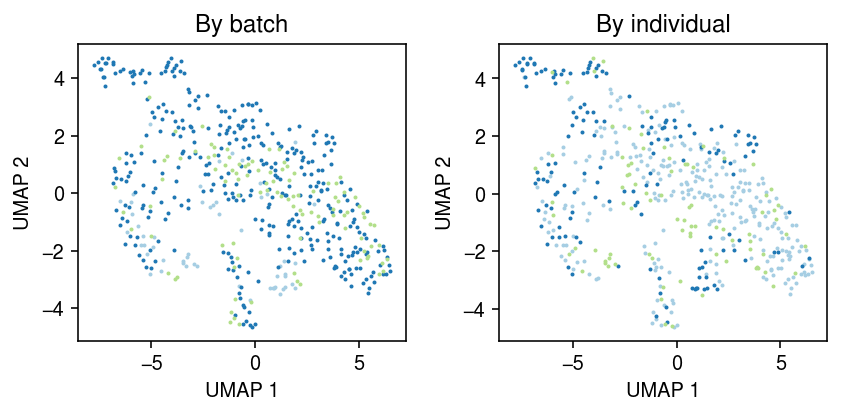
Plot the full data, colored by batch.

sc.pp.neighbors(x)
sc.tl.umap(x, copy=False)

cm = plt.get_cmap('Paired')
plt.clf()
plt.gcf().set_size_inches(3, 3)
for i, k in enumerate(x.obs['batch'].unique()):
  query = x[x.obs['batch'] == k].obsm['X_umap']
  plt.scatter(query[:,0], query[:,1], s=1, c=cm(i), label=k)
plt.title('By batch')
plt.xlabel('UMAP 1')
plt.ylabel('UMAP 2')
plt.tight_layout()

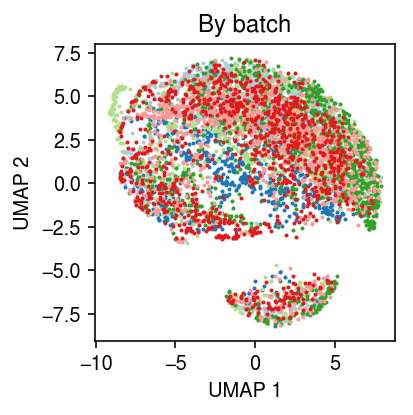
iPSC Drop-Seq data

Is it the case that Fluidigm C1 batch effects are really smaller? Try looking at scRNA-seq of iPSCs generated using Drop-Seq (Selewa et al. 2019).

x = anndata.read_h5ad('/project2/mstephens/aksarkar/projects/singlecell-ideas/data/czi/drop/czi-ipsc-cm.h5ad')

Project \(\ln(x+1)\) into a principal component subspace and compute nearest neighbors.

y = x[x.obs['day'] == 0]
sc.pp.filter_genes(y, min_cells=1)
sc.pp.neighbors(y)
sc.tl.umap(y, copy=False)

Plot the UMAP embedding of the principal component subspace.

cm = plt.get_cmap('Paired')
plt.clf()
plt.gcf().set_size_inches(3, 3)
for i, k in enumerate(y.obs['ind'].unique()):
  query = y[y.obs['ind'] == k].obsm['X_umap']
  plt.scatter(query[:,0], query[:,1], s=1, c=cm(i), label=k)
plt.legend(markerscale=8, handletextpad=0, frameon=False)
plt.title('By donor')
plt.xlabel('UMAP 1')
plt.ylabel('UMAP 2')
plt.tight_layout()

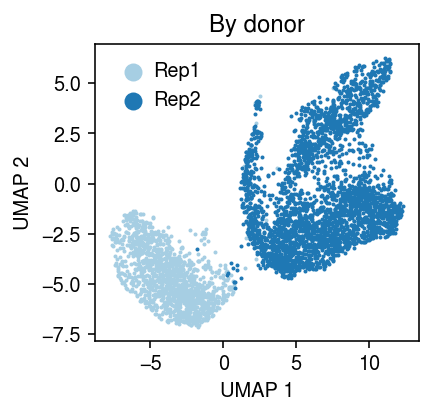
Fit PVAE.

s = y.X.sum(axis=1)
rep = pd.get_dummies(y.obs['ind'])
dataset = td.TensorDataset(
  torch.tensor(s.A.ravel()),
  torch.tensor(y.X.A),
  torch.tensor(rep.values, dtype=torch.float))
data = td.DataLoader(dataset, batch_size=64, shuffle=True, num_workers=2)

fit = PVAE(input_dim=y.shape[1], latent_dim=10, covar_dim=2).fit(data, n_epochs=10, lr=1e-2)

Estimate the GMVAE latent variables \(E[\mathbf{z}_i \mid \mathbf{x}_i y_i]\), then compute a UMAP embedding of the latent space.

y.obsm['pvae'] = fit.latent(td.DataLoader(dataset, batch_size=128, shuffle=False, num_workers=2))
sc.pp.neighbors(y, use_rep='pvae')
sc.tl.umap(y, copy=False)

Plot the UMAP embedding.

cm = plt.get_cmap('Paired')
plt.clf()
plt.gcf().set_size_inches(3, 3)
for i, k in enumerate(y.obs['ind'].unique()):
  query = y[y.obs['ind'] == k].obsm['pvae']
  plt.scatter(query[:,0], query[:,1], s=1, c=np.array(cm(i)).reshape(1, -1), label=k, zorder=-i)
plt.legend(markerscale=8, handletextpad=0, frameon=False)
plt.title('By donor')
plt.xlabel('UMAP 1')
plt.ylabel('UMAP 2')
plt.tight_layout()

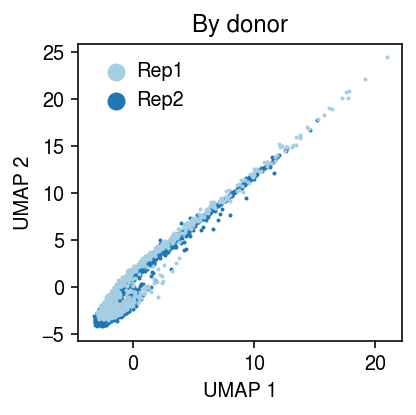
Now, look at fitting PVAE for multiple days and replicates.

y = x[x.obs['day'].isin([0, 3])]
sc.pp.filter_genes(y, min_cells=1)
sc.pp.neighbors(y)
sc.tl.umap(y, copy=False)

cm = plt.get_cmap('Paired')
plt.clf()
plt.gcf().set_size_inches(3.5, 2.5)
for i, (d, k) in enumerate(y.obs.groupby(['day', 'ind']).groups.keys()):
  query = y[np.logical_and(y.obs['day'] == d, y.obs['ind'] == k)].obsm['X_umap']
  plt.scatter(query[:,0], query[:,1], s=1, c=np.array(cm(i)).reshape(1, -1), label=f'Day {d}/{k}', alpha=0.1)
leg = plt.legend(markerscale=4, handletextpad=0, frameon=False, loc='center left', bbox_to_anchor=(1, .5))
for h in leg.legendHandles:
  h.set_alpha(1)
plt.xlabel('UMAP 1')
plt.ylabel('UMAP 2')
plt.tight_layout()

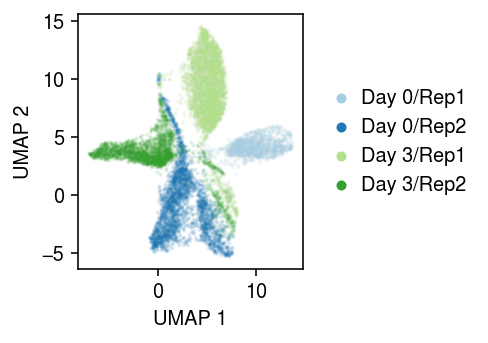
s = y.X.sum(axis=1)
rep = pd.get_dummies(y.obs['ind'])
dataset = td.TensorDataset(
  torch.tensor(s.A.ravel()),
  torch.tensor(y.X.A),
  torch.tensor(rep.values, dtype=torch.float))
data = td.DataLoader(dataset, batch_size=64, shuffle=True, num_workers=1)
fit = PVAE(input_dim=y.shape[1], latent_dim=10, covar_dim=2).fit(data, n_epochs=10, lr=1e-2)

y.obsm['pvae'] = fit.latent(td.DataLoader(dataset, batch_size=64, shuffle=False, num_workers=1))
sc.pp.neighbors(y, use_rep='pvae')
sc.tl.umap(y, copy=False)

cm = plt.get_cmap('Paired')
plt.clf()
plt.gcf().set_size_inches(3.75, 2.5)
for i, (d, k) in enumerate(y.obs.groupby(['day', 'ind']).groups.keys()):
  query = y[np.logical_and(y.obs['day'] == d, y.obs['ind'] == k)].obsm['pvae']
  plt.scatter(query[:,0], query[:,1], s=1, c=np.array(cm(i)).reshape(1, -1), label=f'Day {d}/{k}', alpha=0.5)
plt.legend(markerscale=4, handletextpad=0, frameon=False, loc='center left', bbox_to_anchor=(1, .5))
plt.xlabel('UMAP 1')
plt.ylabel('UMAP 2')
plt.tight_layout()

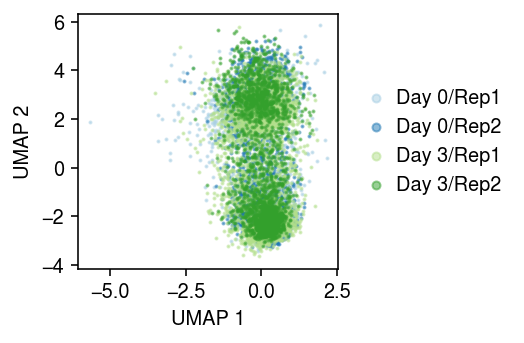
NMF

Instead of PCA, use NMF and normalize to a topic model as the latent space.

m = skd.NMF(n_components=10, solver='mu', beta_loss=1, max_iter=1000, verbose=True)
l = m.fit_transform(x.X)
f = m.components_

weights = l * f.sum(axis=1)
topics = f.T / f.sum(axis=1)
s = weights.sum(axis=1, keepdims=True)
weights /= s

x.obs['topic_scale'] = s
x.obsm['topics'] = weights
x.varm['topics'] = topics
x.write('/project2/mstephens/aksarkar/projects/singlecell-ideas/data/ipsc/ipsc.h5ad')

TODO: this segfaults.

sc.pp.neighbors(x, use_rep='topics')
sc.tl.umap(x, copy=False)

0 - 36d6e328-d507-454e-9ac5-657bf63ae113